练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

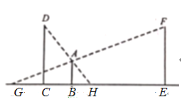
    【题目】如图，一人站在两等高的路灯之间走动，为人在路灯照射下的影子，为人在路灯照射下的影子．当人从点走向点时两段影子之和的变化趋势是（ ）

    A.先变长后变短B.先变短后变长

    C.不变D.先变短后变长再变短

    【答案】C

    【解析】

    连接DF，由题意易得四边形CDFE为矩形.由DF∥GH，可得.又AB∥CD，得出，设=a,DF=b（a,b为常数），可得出，从而可以得出，结合可将DH用含a,b的式子表示出来，最后得出结果.

    解：连接DF，已知CD=EF，CD⊥EG,EF⊥EG,

    ∴四边形CDFE为矩形.

    ∴DF∥GH,

    ∴

    又AB∥CD，∴.

    设=a，DF=b,

    ∴,

    ∴

    ∴

    ∴GH=，

    ∵a,b的长是定值不变，

    ∴当人从点走向点时两段影子之和不变．

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，2，.△ADP沿点A旋转至△ABP′，连接PP′，并延长AP与BC相交于点Q.

    (1)求证：△APP′是等腰直角三角形；

    (2)求∠BPQ的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD内接于⊙O，AC为对角线，∠ACB＝∠ACD

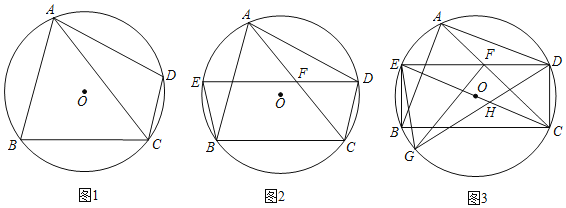
    （1）如图1，求证：AB＝AD；

    （2）如图2，点E在AB弧上，DE交AC于点F，连接BE，BE＝DF，求证：DF＝DC；

    （3）如图3，在（2）的条件下，点G在BC弧上，连接DG，交CE于点H，连接GE，GF，若DE＝BC，EG＝GH＝5，S△DFG＝9，求BC边的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

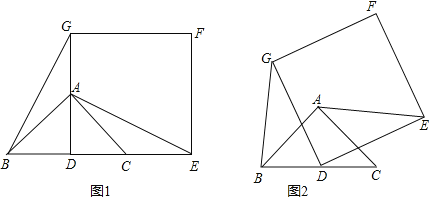
    【题目】如图1，已知是等腰直角三角形，，点D是BC的中点作正方形DEFG，使点A、C分别在DG和DE上，连接AE，BG．

    试猜想线段BG和AE的数量关系是______；

    将正方形DEFG绕点D逆时针方向旋转，

    判断中的结论是否仍然成立？请利用图2证明你的结论；

    若，当AE取最大值时，求AF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正方形的边长为1，为射线上的动点（不与点重合），点关于直线的对称点为，连接，，，．当是等腰三角形时，的值为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线 （a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：

    ①4ac＜b2；

    ②方程 的两个根是x1=﹣1，x2=3；

    ③3a+c＞0

    ④当y＞0时，x的取值范围是﹣1≤x＜3

    ⑤当x＜0时，y随x增大而增大

    其中结论正确的个数是（　　）

    A. 4个 B. 3个 C. 2个 D. 1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A，B，C，D按顺时针方向排列)，已知AB＝BC＝CD，∠ABC＝100°，∠CAD＝40°，则∠BCD的度数为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

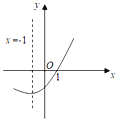
    【题目】如图是二次函数y＝ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c＝0；②b＞2a；③方程ax2+bx+c＝0的两根分别为－3和1；④a－2b+c≥0，其中正确的命题是（　　）

    A.①②③B.①④C.①③D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点D是Rt△ABC斜边AB的中点，过点B、C分别作BE∥CD，CE∥BD．

    （1）若∠A=60°，AC=，求CD的长；

    （2）求证：BC⊥DE．

    查看答案和解析>>

    同步练习册答案