
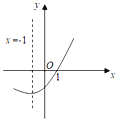
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为-3和1;④a-2b+c≥0,其中正确的命题是( )
A.①②③B.①④C.①③D.①③④
【答案】C
【解析】
根据二次函数的图象可知抛物线开口向上,对称轴为x=-1,且过点(1,0),根据对称轴可得抛物线与x轴的另一个交点为(-3,0),把(1,0)代入可对①做出判断;由对称轴为x=-1,可对②做出判断;根据二次函数与一元二次方程的关系,可对③做出判断;根据a、c的符号,以及对称轴可对④做出判断;最后综合得出答案.
解:由图象可知:抛物线开口向上,对称轴为直线x=-1,过(1,0)点,
把(1,0)代入y=ax2+bx+c得,a+b+c=0,因此①正确;
对称轴为直线x=-1,即:![]() 整理得,b=2a,因此②不正确;
整理得,b=2a,因此②不正确;
由抛物线的对称性,可知抛物线与x轴的两个交点为(1,0)(-3,0),因此方程ax2+bx+c=0的两根分别为-3和1;故③是正确的;
由a>0,b>0,c<0,且b=2a,则a-2b+c=a-4a+c=-3a+c<0,因此④不正确;
故选:C.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为![]() 的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程
的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程![]() ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解.利用上述材料给你的启示,解下列方程;
的解.利用上述材料给你的启示,解下列方程;
(1)![]() ;
;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
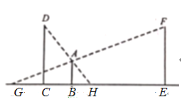
【题目】如图,一人站在两等高的路灯之间走动,![]() 为人
为人![]() 在路灯
在路灯![]() 照射下的影子,
照射下的影子,![]() 为人
为人![]() 在路灯
在路灯![]() 照射下的影子.当人从点
照射下的影子.当人从点![]() 走向点
走向点![]() 时两段影子之和
时两段影子之和![]() 的变化趋势是( )
的变化趋势是( )
A.先变长后变短B.先变短后变长
C.不变D.先变短后变长再变短
查看答案和解析>>
科目:初中数学 来源: 题型:
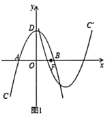
【题目】如图1.在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,顶点为
两点,顶点为![]() ,设点
,设点![]() 是
是![]() 轴的正半轴上一点,将抛物线
轴的正半轴上一点,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.
![]() 求抛物线
求抛物线![]() 的函数表达式:
的函数表达式:
![]() 若抛物线
若抛物线![]() 与抛物线
与抛物线![]() 在
在![]() 轴的右侧有两个不同的公共点,求
轴的右侧有两个不同的公共点,求![]() 的取值范围.
的取值范围.
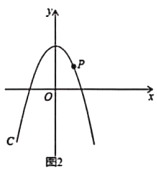
![]() 如图2,
如图2,![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上一点,它到两坐标轴的距离相等,点
上一点,它到两坐标轴的距离相等,点![]() 在抛物线
在抛物线![]() 上的对应点
上的对应点![]() ,设
,设![]() 是
是![]() 上的动点,
上的动点,![]() 是
是![]() 上的动点,试探究四边形
上的动点,试探究四边形![]() 能否成为正方形?若能,求出
能否成为正方形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量y与销售单价x之间的关系可以近似地看作一次函数:![]() .
.
(1)该文具店这种笔记本每月获得利润为w元,求每月获得的利润w元与销售单价x之间的函数关系式;
(2)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,E为AC上一点,直线ED与AB延长线交于点F,若∠CDE=∠DAC,AC=12.
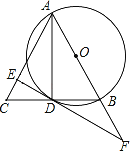
(1)求⊙O半径;
(2)求证:DE为⊙O的切线;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
操作与发现:
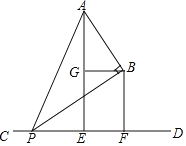
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com