
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为![]() 的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程
的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程![]() ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解.利用上述材料给你的启示,解下列方程;
的解.利用上述材料给你的启示,解下列方程;
(1)![]() ;
;
(2)![]() .
.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)
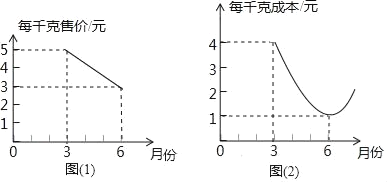
(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AB、AC为一边,向外作正方形ABEF和正方形AGHC像这样的两个正方形称为△ABC的“依伴正方形”
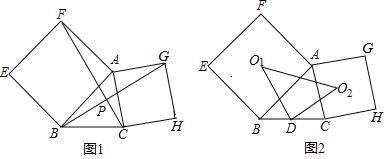
(1)如图1,连接BG,CF相交于点P,求证:BG=CF且BG⊥CF;
(2)如图2,点D是BC的中点,两个依伴正方形的中心分别为O1,O2连结O1D,O2D,O1O2:,判断△DO1O2的形状并说明由;
(3)如图2,若AB=6,AC=![]() ,∠BAC=60°,求O1O2的长.
,∠BAC=60°,求O1O2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C是线段AB上一点,AC=![]() AB,BC为⊙O的直径.
AB,BC为⊙O的直径.
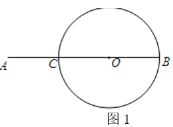
(1)在图1直径BC上方的圆弧上找一点P,使得PA=PB;(用尺规作图,保留作图痕迹,不要求写作法)
(2)连接PA,求证:PA是⊙O的切线;
(3)在(1)的条件下,连接PC、PB,∠PAB的平分线分别交PC、PB于点D、E.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,以点![]()
![]() 为圆心,以3为半径的圆,分别交
为圆心,以3为半径的圆,分别交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 轴负半轴于点
轴负半轴于点![]()
![]() .
.
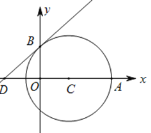
(1)求![]() 两点的坐标;
两点的坐标;
(2)求证:直线![]() 是⊙
是⊙![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,AC为对角线,∠ACB=∠ACD
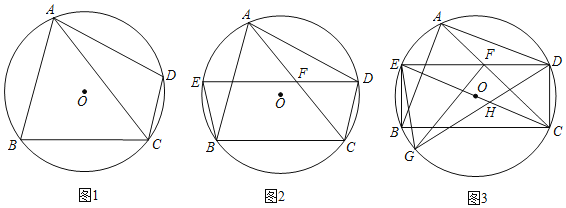
(1)如图1,求证:AB=AD;
(2)如图2,点E在AB弧上,DE交AC于点F,连接BE,BE=DF,求证:DF=DC;
(3)如图3,在(2)的条件下,点G在BC弧上,连接DG,交CE于点H,连接GE,GF,若DE=BC,EG=GH=5,S△DFG=9,求BC边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
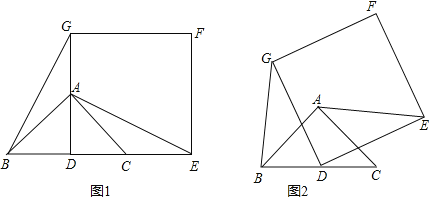
【题目】如图1,已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点D是BC的中点
,点D是BC的中点![]() 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
![]() 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______;
![]() 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转![]() ,
,
![]() 判断
判断![]() 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论;
![]() 若
若![]() ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为-3和1;④a-2b+c≥0,其中正确的命题是( )
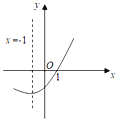
A.①②③B.①④C.①③D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com