
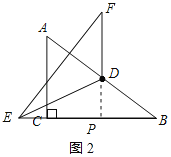
【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D是AB的中点,E是直线BC上一点,把△BDE沿直线ED翻折后,点B落在点F处,当FD⊥BC时,线段BE的长为_____.

【答案】![]() 或5
或5
【解析】
分点F在BC下方,点F在BC上方两种情况讨论,由勾股定理可BC=4,由平行线分线段成比例可得![]() ,求出FP,由勾股定理可求BE的长.
,求出FP,由勾股定理可求BE的长.
解:若点F在BC下方时,DF与BC交于点P,如图1所示:
∵∠C=90°,AC=3,AB=5,
∴BC=![]() =
=![]() =4,
=4,
∵点D是AB的中点,
∴BD=![]() BA=
BA=![]() ,
,
∵FD⊥BC,∠C=90°
∴FD∥AC
∴![]() ,
,
∴BP=PC=![]() BC=2,DP=
BC=2,DP=![]() AC=
AC=![]() ,
,
∵△BDE沿直线ED翻折,
∴FD=BD=![]() ,FE=BE,
,FE=BE,
∴FP=FD﹣DP=1,
∴在Rt△FPE中,EF2=FP2+PE2,
∴BE2=1+(2﹣BE)2,
解得:BE=![]() ;
;
若点F在BC上方时,FD的延长线交BC于点P,如图2所示:
FP=DP+FD=![]() +
+![]() =4,
=4,
在Rt△EFP中,EF2=FP2+EP2,
∴BE2=16+(BE﹣2)2,
解得:BE=5
故答案为:![]() 或5.
或5.



科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
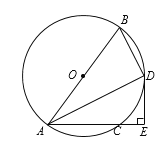
(1)求证:DE是⊙O的切线;
(2)若BD=3,AD=4,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
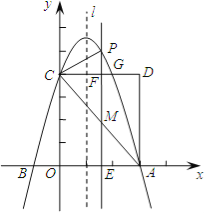
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
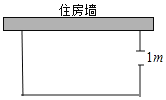
【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的动点(点
上的动点(点![]() 不与点
不与点![]() 重合),点
重合),点![]() 在边
在边![]() 的延长线上,
的延长线上,![]() ,
,![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .
.
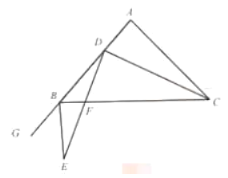
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)点![]() 在边
在边![]() 上运动的过程中,
上运动的过程中,![]() 的值是否会发生变化?如果不变化,请求
的值是否会发生变化?如果不变化,请求![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进了一种新款小电器,为了寻找合适的销售价格,进行了为期5周的试营销,试营销的情况如表所示:
第1周 | 第2周 | 第3周 | 第4周 | 第5周 | |
售价/(元/台) | 50 | 40 | 60 | 55 | 45 |
销售/台 | 360 | 420 | 300 | 330 | 390 |
已知该款小电器的进价每台30元,设该款小电器每台的售价为x元,每周的销量为y台.
(1)观察表中的数据,推断y与x满足什么函数关系,并求出这个函数关系式;
(2)若想每周的利润为9000元,则其售价应定为多少元?
(3)若每台小电器的售价不低于40元,但又不能高于进价的2倍,则如何定价才能更快地减少库存?此时每周最多可销售多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转60°,得到△AED,点B、C的对应点分别是E、D.F为AC的中点,连接BF、DF、BE,DF与EA相交于点G,BE与AC相交于点H.
(1)如图1,求证:四边形BFDE为平行四边形;
(2)如图2,连接CE,在不添加任何辅助线与字母的情况下,请直接写出所有与△AEC全等的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
①AD_____AN(填“>”,“=”或“<”);
②AB=8,ON=1,⊙O的半径为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(1,0),B(4,0)与
经过点A(1,0),B(4,0)与![]() 轴交于点C.
轴交于点C.
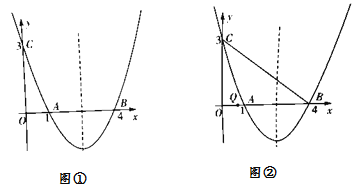
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com