
【题目】某商店购进了一种新款小电器,为了寻找合适的销售价格,进行了为期5周的试营销,试营销的情况如表所示:
第1周 | 第2周 | 第3周 | 第4周 | 第5周 | |
售价/(元/台) | 50 | 40 | 60 | 55 | 45 |
销售/台 | 360 | 420 | 300 | 330 | 390 |
已知该款小电器的进价每台30元,设该款小电器每台的售价为x元,每周的销量为y台.
(1)观察表中的数据,推断y与x满足什么函数关系,并求出这个函数关系式;
(2)若想每周的利润为9000元,则其售价应定为多少元?
(3)若每台小电器的售价不低于40元,但又不能高于进价的2倍,则如何定价才能更快地减少库存?此时每周最多可销售多少台?
【答案】(1)y与x满足一次函数关系,y=﹣6x+660;(2)若想每周的利润为9000元,则其售价应定为每台60元或每台80元;(3)定价为40元/台时,才能更快地减少库存,此时每周最多可销售420台
【解析】
(1)根据题意和表格中的数据可以判断出y与x的函数关系式,并求出这个函数关系式;
(2)根据题意可以得到每周的利润为9000元,则其售价应定为多少元;
(3)根据题意和(1)中的函数关系式,利用一次函数的性质可以解答本题.
解:(1)y与x满足一次函数关系,
设y与x的函数关系式为y=kx+b,
![]() ,得
,得![]() ,
,
即这个函数关系式是y=﹣6x+660;
(2)(x﹣30)(﹣6x+660)=9000,
解得,x1=60,x2=80,
答:若想每周的利润为9000元,则其售价应定为每台60元或每台80元;
(3)由题意可得,
40≤x≤30×2,
即40≤x≤60,
∵y=﹣6x+660,
∴当x=40时,y取得最大值,此时y=420,
答:定价为40元/台时,才能更快地减少库存,此时每周最多可销售420台.


科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.
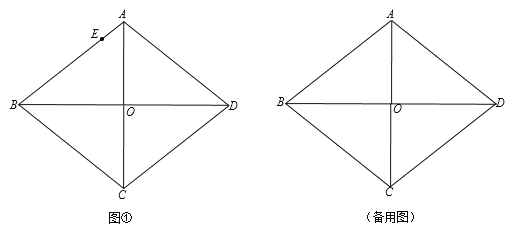
(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,D为边AB上一点,连接CD,在线段CD上取一点E,以AE为直角边作等腰直角△AEF,使∠EAF=90°,连接BF交CD的延长线于点P.

(1)探索:CE与BF有何数量关系和位置关系?并说明理由;
(2)如图2,若AB=2,AE=1,把△AEF绕点A顺时针旋转至△AE'F′,当∠E′AC=60°时,求BF′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D是AB的中点,E是直线BC上一点,把△BDE沿直线ED翻折后,点B落在点F处,当FD⊥BC时,线段BE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中,线段AB的端点均在小正方形的顶点上.

(1)在图中画出以AB为底的等腰三角形ABC,点C在小正方形的顶点上,且△ABC的面积是7.5;
(2)在(1)的条件下,在图中画出以AC为斜边的直角三角形ACE(AE<EC),点E在小正方形的顶点上,且△ACE的面积是5,连接EB,并直接写出tan∠AEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
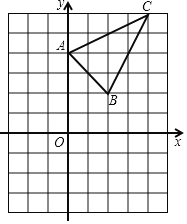
【题目】如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,4),B(2,2),C(4,6)(正方形网格中,每个小正方形的边长为1)
(1)画出△ABC向下平移5个单位得到的△A1B1C1,并写出点B1的坐标;
(2)以点O为位似中心,在第三象限画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为1:2,直接写出点C2的坐标和△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.

(1)求∠PCQ的度数;
(2)当AB=4,AP=![]() 时,求PQ的大小;
时,求PQ的大小;
(3)当点P在线段AC上运动时(P不与A,C重合),求证:2PB2=PA2+PC2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区检票口有A、B、C、D共4个检票通道.甲、乙两人到该景区游玩,两人分别从4个检票通道中随机选择一个检票.
(1)甲选择A检票通道的概率是 ;
(2)求甲乙两人选择的检票通道恰好相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com