
【题目】如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.
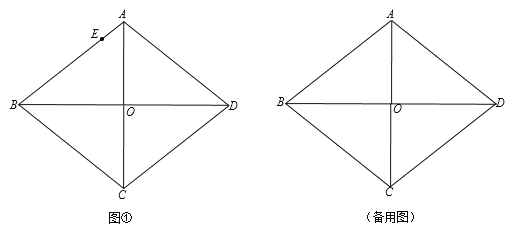
(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
【答案】(1)见解析;(2)①当m=0时,存在1个矩形EFGH;②当0<m<![]() 时,存在2个矩形EFGH;③当m=
时,存在2个矩形EFGH;③当m=![]() 时,存在1个矩形EFGH;④当
时,存在1个矩形EFGH;④当![]() <m≤
<m≤![]() 时,存在2个矩形EFGH;⑤当
时,存在2个矩形EFGH;⑤当![]() <m<5时,存在1个矩形EFGH;⑥当m=5时,不存在矩形EFGH.
<m<5时,存在1个矩形EFGH;⑥当m=5时,不存在矩形EFGH.
【解析】
(1)以O点为圆心,OE长为半径画圆,与菱形产生交点,顺次连接圆O与菱形每条边的同侧交点即可;
(2)分别考虑以O为圆心,OE为半径的圆与每条边的线段有几个交点时的情形,共分五种情况.
(1)如图①,如图②(也可以用图①的方法,取⊙O与边BC、CD、AD的另一个交点即可)

(2)∵O到菱形边的距离为![]() ,当⊙O与AB相切时AE=
,当⊙O与AB相切时AE=![]() ,当过点A,C时,⊙O与AB交于A,E两点,此时AE=
,当过点A,C时,⊙O与AB交于A,E两点,此时AE=![]() ×2=
×2=![]() ,根据图像可得如下六种情形:
,根据图像可得如下六种情形:
①当m=0时,如图,存在1个矩形EFGH;

②当0<m<![]() 时,如图,存在2个矩形EFGH;
时,如图,存在2个矩形EFGH;


③当m=![]() 时,如图,存在1个矩形EFGH;
时,如图,存在1个矩形EFGH;

④当![]() <m≤
<m≤![]() 时,如图,存在2个矩形EFGH;
时,如图,存在2个矩形EFGH;

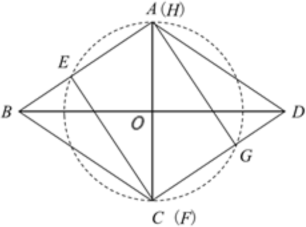
⑤当![]() <m<5时,如图,存在1个矩形EFGH;
<m<5时,如图,存在1个矩形EFGH;

⑥当m=5时,不存在矩形EFGH.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=CB,D是边AC的中点,过点D做DE⊥BC于E.
(1)以边AB为直径作⊙O,作图要求:尺规作图,保留作图痕迹,不写作法;
(2)在(1)条件下,判断DE与圆O是否相切?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
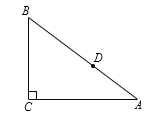
【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴正半轴上,点A与原点重合,点D的坐标是 (3,4),反比例函数y=![]() (k≠0)经过点C,则k的值为( )
(k≠0)经过点C,则k的值为( )
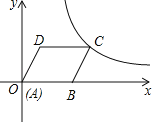
A.12B.15C.20D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E点.

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=60°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com