
【题目】解方程
(1)x2﹣2x=5
(2)(3﹣y)2+y2=9
(3)2x2﹣7x+1=0
【答案】(1)x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ;(2)y1=3,y2=0;(3)x1=
;(2)y1=3,y2=0;(3)x1=![]() ,x2=
,x2=![]() .
.
【解析】
(1)先配方,再开方,即可得出两个一元一次方程,求出方程的解即可;
(2)移项后因式分解,即可得出两个一元一次方程,求出方程的解即可;
(3)先求出b2﹣4ac的值,再代入公式求出即可.
解:(1)配方得:x2﹣2x+1=5+1,
(x﹣1)2=6,
开方得:x﹣1=![]() ,
,
解得:x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ;
;
(2)移项得:(3﹣y)2+y2﹣9=0,
(y﹣3)2+(y+3)(y﹣3)=0,
(y﹣3)[(y﹣3)+(y+3)]=0,
y﹣3=0,(y﹣3)+(y+3)=0,
解得:y1=3,y2=0;
(3)2x2﹣7x+1=0,
b2﹣4ac=(﹣7)2﹣4×2×1=41>0,
x=![]() ,
,
解得:x1=![]() ,x2=
,x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】一家水果店以每千克2元的价格购进某种水果若干千克,然后以每千克4元的价格出售,每天可售出100千克,通过调查发现,这种水果每千克的售价每降低1元,每天可多售出200千克.
(1)若将这种水果每千克的售价降低![]() 元,则每天销售量是多少千克?(结果用含
元,则每天销售量是多少千克?(结果用含![]() 的代数式表示)
的代数式表示)
(2)若想每天盈利300元,且保证每天至少售出260千克,那么水果店需将每千克的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)(y+2)2-(3y-1)2=0;
(2)5(x-3)2=x2-9;
(3)t2-![]() t+
t+![]() =0.
=0.
(4)2x2+7x+3=0(配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的y与x的部分对应值如表:
的y与x的部分对应值如表:
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(![]() ,2),B(
,2),B(![]() ,3)是抛物线上两点,则
,3)是抛物线上两点,则![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )

A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.
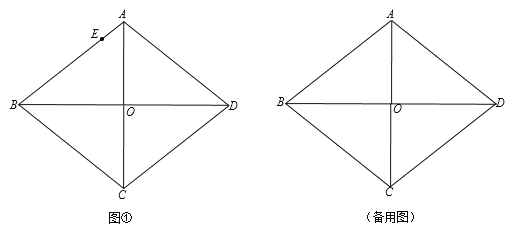
(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
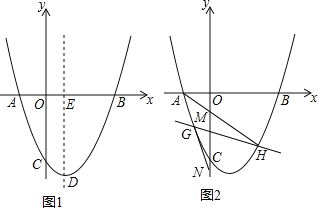
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣4ax﹣6(a>0)与x轴交于A,B两点,且OB=3OA,与y轴交于点C,抛物线的顶点为D,对称轴与x轴交于点E.
(1)求该抛物线的解析式,并直接写出顶点D的坐标;
(2)如图2,直线y=![]() +n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;
+n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;
(3)如图1,点P在线段DE上,作等腰△BPQ,使得PB=PQ,且点Q落在直线CD上,若满足条件的点Q有且只有一个,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com