
 如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时
如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时 分析 (1)①先运用三角形内角和定理,得出∠ABD=∠ECD,再根据∠ABD=22.5°,得到∠ECD=22.5°;②延长CE交BA的延长线于点G,通过判定△ABD≌△ACG,得出BD=CG=2CE即可;
(2)连接CQ,过点Q作QM⊥BP于M,作QN⊥BC于N,在等腰直角△CPF中,求得∠QCP=∠QPC=22.5°,进而得出△PQC中,∠PQC=135°;在四边形QNBM中,根据QM⊥BP,QN⊥BC,∠ABC=45°,得到∠MQN=135°,进而得到∠NQC=∠MQP,根据AAS判定△QPM≌△QCN,得出QM=QN,最后根据角平分线的性质定理的逆定理,得出点Q一定在射线BD上.
解答 解:(1)①∵∠BAC=90°,CE⊥BD,∠ADB=∠CDE,
∴∠ABD=∠ECD,
又∵∠BAC=90°,AB=AC,BD平分∠ABC,
∴∠ABD=22.5°,
∴∠ECD=22.5°;
故答案为:22.5.
②如图,延长CE交BA的延长线于点G,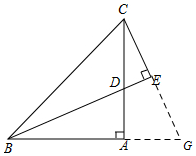
∵BD平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD与△ACG中,
$\left\{\begin{array}{l}{∠DBA=∠ACG}\\{∠BAC=∠CAG}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)点Q一定在射线BD上,
理由:如图,连接CQ,过点Q作QM⊥BP于M,作QN⊥BC于N,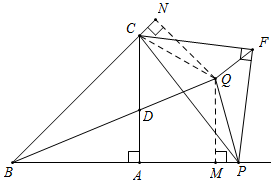
∵QF为∠PFC的角平分线,△CPF为等腰直角三角形,
∴QF为PC的垂直平分线,
∴PQ=QC,
∵Q为∠FPC与∠PFC的角平分线的交点,
∴CQ平分∠FCP,
∵△CPF为等腰直角三角形,
∴∠FCP=∠FPC=45°,
∴∠QCP=∠QPC=22.5°,
∴△PQC中,∠PQC=135°,
∵在四边形QNBM中,QM⊥BP,QN⊥BC,∠ABC=45°,
∴∠MQN=135°,
∴∠MQN=∠PQC,
∴∠NQC=∠MQP,
又∵QC=QP,QM⊥BP,QN⊥BC,
∴△QPM≌△QCN(AAS),
∴QM=QN,
又∵QM⊥BP,QN⊥BC,
∴点Q一定在射线BD上.
点评 本题主要考查了三角形的综合应用,解题时需要运用三角形内角和定理、等腰直角三角形的性质、角平分线的定义以及全等三角形的判定与性质等知识.解决问题的关键是作辅助线,构造全等三角形,根据全等三角形的性质进行推导.解题时注意:到角两边距离相等的点在这个角的平分线上.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
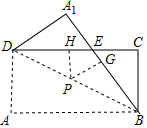 如图,四边形ABCD是长方形,将△ABD沿着BD翻折,点A的对应点为A1,BA1与CD交于点E,点P是线段DB(除去点D和点B)上任意一点,过点P分别作CD和BA1的 垂线,垂足为点G和点H,已知AB=8,AD=4,则PG+PH=4.
如图,四边形ABCD是长方形,将△ABD沿着BD翻折,点A的对应点为A1,BA1与CD交于点E,点P是线段DB(除去点D和点B)上任意一点,过点P分别作CD和BA1的 垂线,垂足为点G和点H,已知AB=8,AD=4,则PG+PH=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
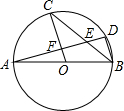 如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:
如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:| A. | ①③⑤ | B. | ②③④ | C. | ②④⑤ | D. | ①③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 张大爷要围成一个矩形花圃.花圃的一边利用墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.
张大爷要围成一个矩形花圃.花圃的一边利用墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
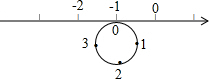 如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上(如圆周上表示数字3的点与数轴上表示-2的点重合…),则数轴上表示-2016的点与圆周上表示数字1的点重合.
如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上(如圆周上表示数字3的点与数轴上表示-2的点重合…),则数轴上表示-2016的点与圆周上表示数字1的点重合.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com