【题目】用指定的方法解方程：
（1）x-2=x(x-2)（因式分解法）
（2）
（用配方法）
（3）
（用公式法）
（4）
（用合适的方法）
【答案】（1）x1=1 ，x2=2;（2）x1=3 ，x2=-1;（3）
;(4) x1=- 
，x2=-5
【解析】
（1）先移项再分解因式，即可得出两个一元一次方程，求出方程的解即可．
(2)根据配方法的步骤，求出方程的解即可．
(3) 先求出b2-4ac的值，再代入公式求出即可；
(4)利用因式分解解方程
解：（1）x-2=x(x-2)
（x-2）（1-x）=0，
x-2=0或1-x=0，
∴x1=2，x2=1；
(2) 
x2-2x=3，
x2-2x+1=4，
（x-1）2=4，
x-1=
x-1=2或x-1=-2
∴x1=3，x2=-1；
(3) 
∴a=2，b=-9，c=8
∴△=b2-4ac=（-9）2-4×2×8=17＞0，
∴
∴
（x-2+2x+3）（x-2-2x-3）=0，
（3x+1）（-x-5）=0，
3x+1=0或-x-5=0，
∴x1=
，x2=-5；
名师指导期末冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF，若菱形ABCD的边长为2cm，∠A=120°，则EF的长为（ ）
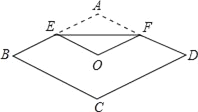
A. 2
B. 2 C. D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现有一段120m的篱笆，准备用这些篱笆借助一段墙角围成如图所示两块面积相同的矩形场地养鸡.
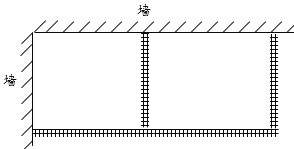
（1）如图所示，若围成的场地总面积为1750m2，则该场地的宽（图中纵向）应为多少？
（2）能不能围成面积为2000m2的场地？若能，求出此时篱笆的宽；若不能，求围成场地面积的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA＝2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
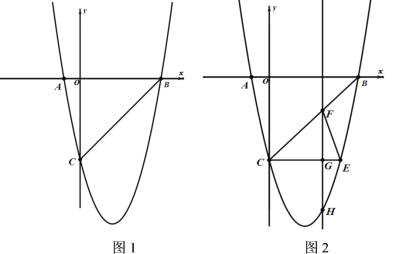
【题目】如图1，在平面直角坐标系中，已知抛物线y=ax2+bx-5与x轴交于A(-1，0)，B(5，0)两点，与y轴交与点C.
(1)求抛物线的函数表达式;
(2)若点D是y轴上的点，且以B、C、D为顶点的三角形与△ABC相似，求点D的坐标;
(3)如图2，CE//x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC、CE分别相交于点F，G，试探求当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知四边形ABCD中，EF分别是AB、AD边上的点，DE与CF交于点G．
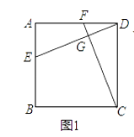
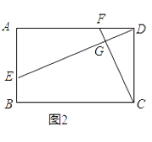
（1）如图1，若四边形ABCD是正方形，且DE⊥CF，求证：DE=CF；
（2）如图2，若四边形ABCD是矩形，且DE⊥CF，求证：
；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
（1）求证：CE＝AD；
（2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
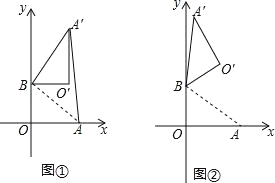
【题目】在平面直角坐标系中，O 为原点，点 A（4，0），点 B（0，3），把△ABO 绕点 B 逆时针旋转，得△A′BO′，点 A、O 旋转后的对应点为 A′、O′，记旋转角为ɑ．
(1)如图 1，若ɑ＝90°，求 AA′的长；
(2)如图 2，若ɑ＝120°，求点 O′的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某小学学生较多，为了便于学生尽快就餐，师生约定：早餐一人一份，一份两样，一样一个，食堂师傅在窗口随机发放（发放的食品价格一样），食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品．
（1）按约定，“小李同学在该天早餐得到两个油饼”是 事件；（可能，必然，不可能）
（2）请用列表或树状图的方法，求出小张同学该天早餐刚好得到猪肉包和油饼的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com