
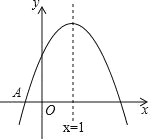
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣![]() ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )
A.①③④ B.①②③ C.①②④ D.①②③④
【答案】B
【解析】
试题分析:①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),当x>3时,y<0,故①正确;
②抛物线开口向下,故a<0,∵x=﹣![]() =1,∴2a+b=0.∴3a+b=0+a=a<0,故②正确;
=1,∴2a+b=0.∴3a+b=0+a=a<0,故②正确;
③设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,令x=0得:y=﹣3a.
∵抛物线与y轴的交点B在(0,2)和(0,3)之间,∴2≤﹣3a≤3.
解得:﹣1≤a≤﹣![]() ,故③正确;
,故③正确;
④.∵抛物线y轴的交点B在(0,2)和(0,3)之间,∴2≤c≤3,由4ac﹣b2>8a得:4ac﹣8a>b2,
∵a<0,∴c﹣2<![]() ,∴c﹣2<0,∴c<2,与2≤c≤3矛盾,故④错误.
,∴c﹣2<0,∴c<2,与2≤c≤3矛盾,故④错误.
故选:B.


科目:初中数学 来源: 题型:
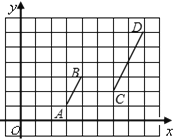
【题目】线段AB、CD在平面直角坐标系中位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(a、b),则直线OP与线段CD的交点坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,抛物线y=a( x-4 )2-16(a>0)交x轴于点E,F(E在F的左边),交y轴于点C,对称轴MN交x轴于点H;直线y=![]() x+b分别交x,y轴于点A,B.
x+b分别交x,y轴于点A,B.
(1)写出该抛物线顶点D的坐标及点C的纵坐标(用含a的代数式表示).
(2)若AF=AH=OH,求证:∠CEO=∠ABO.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是数值转换机的示意图,图②是小亮按照其对应关系画出的y与x的函数图象.已知点A的坐标为(0,3),点B的横坐标为4.
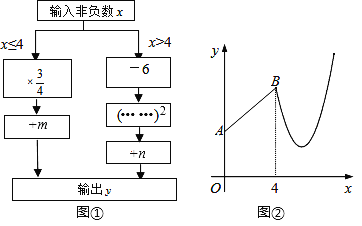
(1)求m、n的值.
(2)求输出y的最小值.
(3)当y=4时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
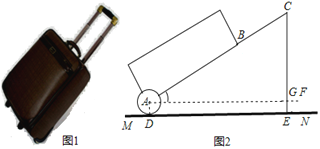
【题目】有一只拉杆式旅行箱如图1,其侧面示意图如图2所示,已知箱体长AB=50 cm,拉杆BC的伸长距离最大时可达35 cm,点A、B、C在同一条直线上,在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面切于点D,在拉杆伸长至最大的情况下,当点B到水平地面MN的距离为38 cm时,点C到水平面的距离CE为59 cm.设AF∥MN,AF交CE于点G(精确到1 cm,参考数据:sin64°≈0.90,cos64°≈0.39,tan64°≈2.1)
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为80 cm,∠CAF=64°.求此时拉杆BC的伸长距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2﹣(m﹣1)x﹣1=0.
(1)求证:这个一元二次方程总有两个实数根;
(2)若二次函数y=mx2﹣(m﹣1)x﹣1有最大值0,则m的值为 ;
(3)若x1、x2是原方程的两根,且![]() =2x1x2+1,求m的值.
=2x1x2+1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com