
【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD. 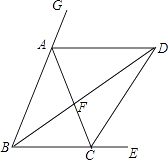
(1)求证:∠BDC= ![]() ∠BAC;
∠BAC;
(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
【答案】
(1)解:∵BD、CD分别平分∠EBA、∠ECA,BD交AC于F,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,∠BAC+∠ABC=∠ACE,
∠ACE,∠BAC+∠ABC=∠ACE,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠BAC+
∠BAC+ ![]() ∠ABC,
∠ABC,
∴∠BDC= ![]() ∠BAC
∠BAC
(2)解:△ABD为等腰三角形,证明如下:
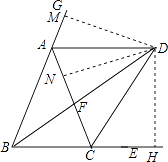
作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H
∵BD、CD分别平分∠EBA、∠ECA,
∴DM=DH,DN=DH,
∴DM=DN,
∴AD平分∠CAG,即∠GAD=∠CAD,
∵∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,
∴∠GAD+∠CAD=∠ABC+∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠GAD=∠ABC,
∴AD∥BC,
∴∠ADB=∠DBC,
又∵∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴△ABD为等腰三角形
(3)解:∵AF=BF,
∴∠BAF=∠ABF= ![]() ∠ABC,
∠ABC,
∵∠BAF+∠ABC+∠ACB=180°,∠ABC=∠ACB,
∴ ![]() ∠ABC=180°,
∠ABC=180°,
∴∠ABC=72°.
【解析】(1)根据角平分线的定义得到∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠BAC+
∠BAC+ ![]() ∠ABC,等量代换即可得到结论;(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC,由平行线的性质得到∠ADB=∠DBC,证得∠ABD=∠ADB,即可得到结论;(3)根据等腰三角形的性质得到∠BAF=∠ABF=
∠ABC,等量代换即可得到结论;(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC,由平行线的性质得到∠ADB=∠DBC,证得∠ABD=∠ADB,即可得到结论;(3)根据等腰三角形的性质得到∠BAF=∠ABF= ![]() ∠ABC,根据三角形的内角和即可得到结论.
∠ABC,根据三角形的内角和即可得到结论.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】判定两角相等,不对的是( )
A.对顶角相等
B.两直线平行,同位角相等
C.∵∠1=∠2,∠2=∠3,∴∠1=∠3
D.两条直线被第三条直线所截,内错角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下: 如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.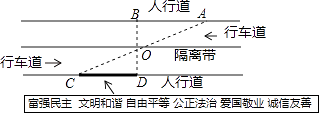
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有25名同学参加某项比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的()
A. 最高分 B. 中位数 C. 方差 D. 平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一次函数是正比例函数
B. 正比例函数是一次函数
C. 不是正比例函数就一定不是一次函数
D. 正比例函数不一定是一次函数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率给出的统计图如图所示,则符合这一结果的实验可能是( )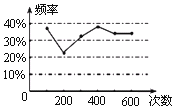
A.掷一枚正六面体的骰子,出现5点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com