
【题目】已知抛物线与x轴交于A(6,0)、B(![]() ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
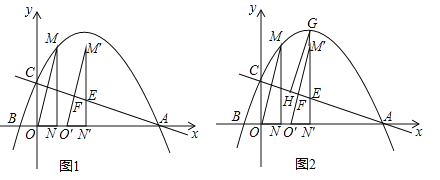
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)①1;②t=2时,EH最大值为
;(2)①1;②t=2时,EH最大值为![]() .
.
【解析】
试题分析:(1)设抛物线解析式为![]() ,把点M(1,3)代入即可求出a,进而解决问题.
,把点M(1,3)代入即可求出a,进而解决问题.
(2))①如图1中,AC与OM交于点G.连接EO′,首先证明△AOC∽△MNO,推出OM⊥AC,在RT△EO′M′中,利用勾股定理列出方程即可解决问题.
②由△GHE∽△AOC得![]() =
=![]() =
=![]() ,所以EG最大时,EH最大,构建二次函数求出EG的最大值即可解决问题.
,所以EG最大时,EH最大,构建二次函数求出EG的最大值即可解决问题.
试题解析:(1)设抛物线解析式为![]() ,把点M(1,3)代入得a=
,把点M(1,3)代入得a=![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∴
,∴![]() .
.
(2)①如图1中,AC与OM交于点G.连接EO′.∵AO=6,OC=2,MN=3,ON=1,∴![]() =3,∴
=3,∴![]() ,∵∠AOC=∠MON=90°,∴△AOC∽△MNO,∴∠OAC=∠NMO,∵∠NMO+∠MON=90°,∴∠MON+∠OAC=90°,∴∠AGO=90°,∴OM⊥AC,∵△M′N′O′是由△MNO平移所得,∴O′M′∥OM,∴O′M′⊥AC,∵M′F=FO′,∴EM′=EO′,∵EN′∥CO,∴
,∵∠AOC=∠MON=90°,∴△AOC∽△MNO,∴∠OAC=∠NMO,∵∠NMO+∠MON=90°,∴∠MON+∠OAC=90°,∴∠AGO=90°,∴OM⊥AC,∵△M′N′O′是由△MNO平移所得,∴O′M′∥OM,∴O′M′⊥AC,∵M′F=FO′,∴EM′=EO′,∵EN′∥CO,∴![]() ,∴
,∴![]() ,∴EN′=
,∴EN′=![]() (5﹣t),在RT△EO′M′中,∵O′N′=1,EN′=
(5﹣t),在RT△EO′M′中,∵O′N′=1,EN′=![]() (5﹣t),EO′=EM′=
(5﹣t),EO′=EM′=![]() ,∴
,∴![]() ,∴t=1.
,∴t=1.
②如图2中,∵GH∥O′M′,O′M′⊥AC,∴GH⊥AC,∴∠GHE=90°,∵∠EGH+∠HEG=90°,∠AEN′+∠OAC=90°,∠HEG=∠AEN′,∴∠OAC=∠HGE,∵∠GHE=∠AOC=90°,∴△GHE∽△AOC,∴![]() ,∴EG最大时,EH最大,∵EG=GN′﹣EN′=
,∴EG最大时,EH最大,∵EG=GN′﹣EN′=![]() =
=![]() =
=![]() ,∴t=2时,EG最大值=
,∴t=2时,EG最大值=![]() ,∴EH最大值=
,∴EH最大值=![]() ,∴t=2时,EH最大值为
,∴t=2时,EH最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】三角形ABC三个顶点的坐标分别是A(-4,-1),B(1,1),C(-1,4),将三角形ABC向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A. (2,2),(3,4),(1,7) B. (-2,2),(4,3),(1,7)
C. (-2,2),(3,4),(1,7) D. (2,-2),(3,3),(1,7)
查看答案和解析>>
科目:初中数学 来源: 题型:
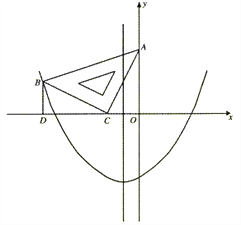
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为 (-1,0) .如图所示,B点在抛物线y=![]() x2+
x2+![]() x-2图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
x-2图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com