
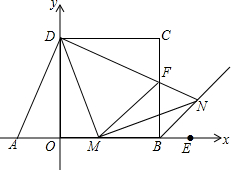
 在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O,B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.
在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O,B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.分析 (1)由正方形的性质可以得出OB=BC=OD就可以求出点C的坐标;
(2)在OD上取一点G,使OG=OM,就可以得出DG=BM,从而得出△GDM≌△BMN,就可以得出结论;
(3)由旋转可以得出△FCD≌△AOD,就可以得出OA=FC,∠ADM=∠CDM,进而得出△DMA≌△DMF,就可以得出AM=FM而得出结论.
解答 解:(1)∵四边形OBCD是正方形,
∴OB=BC=OD,∠DOB=∠OBC=∠C=90°.
∵D(0,2),
∴OD=2,
∴OB=BC=OD=2,
∴C(2,2);
(2)在OD上取一点G,使OG=OM,
∴∠OGM=∠OMG=45°,
∴∠DGM=135°.
∵OD=OB,
∴OD-OG=OB-OM,
∴GD=BM.
∵MN⊥DM,
∴∠DMN=90°,
∴∠DMO+∠NMB=90°.
∵∠DMO+∠ODM=90°,
∴∠ODM=∠BMN.
∵BN平分∠CBE,
∴∠NBE=$\frac{1}{2}$×90°=45°,
∴∠MBN=135°,
∴∠DGM=∠MBN.
在△GDM和△BMN中
$\left\{\begin{array}{l}{∠DGM=∠MBN}\\{GD=BM}\\{∠ODM=∠BMN}\end{array}\right.$,
∴△GDM≌△BMN(ASA),
∴MD=MN;
(3)OM+CF=MF
理由:∵MD=MN,∠DMN=90°,
∴∠MDN=45°,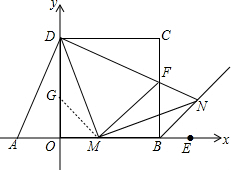
∴∠ODM+∠FDC=45°.
∵△DCF绕点D顺时针旋转90°得△DOA,
∴△DCF≌△DOA,
∴AO=FC,∠ADO=∠FDC,AD=FD.
∴∠ADO+∠MDO=45°,
即∠ADM=45°.
∴∠ADM=∠CDM.
在△DMA和△DMF中
$\left\{\begin{array}{l}{AD=FD}\\{∠ADM=∠CDM}\\{DM=DM}\end{array}\right.$,
∴△DMA≌△DMF(SAS),
∴AM=FM.
∵AM=AO+MO,
∴AM=CF+MO,
∴OM+CF=MF.
点评 本题考查了正方形的性质的运用,旋转的性质的运用,全等三角形的判定及性质的运用,角平分线的性质的运用,解答时证明三角形全等是关键.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
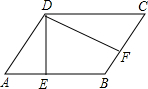 如图,李军家承包了一块菜地,用来种菜,菜地的形状为平行四边形.经测量其周长为36m,从钝角顶点处向AB、BC引的两条高DE、DF分别为5m、7m,求这块平行四边形菜地的面积.
如图,李军家承包了一块菜地,用来种菜,菜地的形状为平行四边形.经测量其周长为36m,从钝角顶点处向AB、BC引的两条高DE、DF分别为5m、7m,求这块平行四边形菜地的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
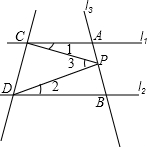 如图,直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
如图,直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com