
 的最小值是
的最小值是A. | B.1 | C.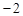 | D.2 |
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源:不详 题型:解答题
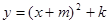 的图象,其顶点坐标为M(1,-4).
的图象,其顶点坐标为M(1,-4).
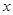 轴的交点A,B的坐标;
轴的交点A,B的坐标; 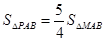 ,若存在,求出P点的坐标;若不存在,请说明理由;
,若存在,求出P点的坐标;若不存在,请说明理由;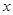 轴下方的部分沿
轴下方的部分沿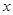 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线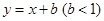 与此图象有两个公共点时,
与此图象有两个公共点时,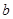 的取值范围.
的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 在平面直角坐标系中的位置如图所示,
在平面直角坐标系中的位置如图所示, ,
, .抛物线
.抛物线 (
( )经过点
)经过点 和点
和点 ,与
,与 轴分别交于点
轴分别交于点 、
、 (点
(点 在点
在点 左侧),且
左侧),且 ,则下列结论:①
,则下列结论:① ;②
;② ;③
;③ ;④
;④ ;⑤连接
;⑤连接 、
、 ,则
,则 ,其中正确结论的个数为
,其中正确结论的个数为
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 的值最大.若存在,求出T点坐标;若不存在,请说明理由.
的值最大.若存在,求出T点坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
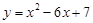 的最大值.他画图研究后发现,
的最大值.他画图研究后发现,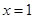 和
和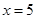 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对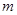 进行分类讨论.
进行分类讨论.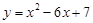 的对称轴为直线
的对称轴为直线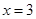 ,
,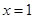 和
和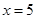 时的函数值相等.
时的函数值相等.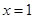 时,
时,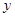 的最大值为2;
的最大值为2;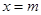 时,
时,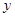 的最大值为
的最大值为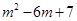 .
.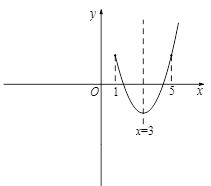
 ≤x≤4时,二次函数
≤x≤4时,二次函数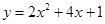 的最大值为_______;
的最大值为_______;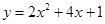 的最大值;
的最大值;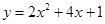 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
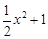 、y=
、y=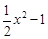 所截.当直线L向右平移2个单位时,直线L被两条抛物线所截得的线段扫过的图形面积为 __ 平方单位。
所截.当直线L向右平移2个单位时,直线L被两条抛物线所截得的线段扫过的图形面积为 __ 平方单位。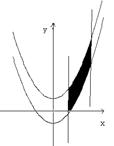
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com