
如图,在□ABCD中,∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G.
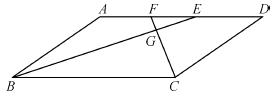
(1)求证:BE⊥CF;
(2)若AB=3,BC=5,CF=2,求BE的长.
(1)证明:∵BE平分∠ABC,
∴∠CBE= ∠ABC.
∠ABC.
同理∠BCF= ∠BCD.
∠BCD.
∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠CBE+∠BCF= ∠ABC+
∠ABC+ ∠BCD=
∠BCD= (∠ABC+∠BCD)=90°,
(∠ABC+∠BCD)=90°,
∴∠CGB=90°,即BE⊥CF.
(2)过点E作EP∥FC,交BC的延长线于点P,则四边形CPEF是平行四边形.
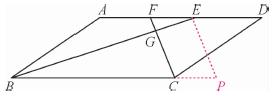
∵BE平分∠ABC,∴∠ABE=∠CBE.
在□ABCD中,∵AD∥BC,∴∠AEB=∠CBE,
∴∠ABE=∠AEB,∴AE=AB=3.
同理DF=DC=3.
∴EF=AE+DF-AD=1,
∴CP=EF=1,EP=CF=2,BP=6.
又由(1)已证得BE⊥CF,∴BE⊥EP,
∴在Rt△BPE中,BE=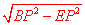 =
=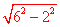 =4
=4 .
.


科目:初中数学 来源: 题型:
四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC,②AD=BC,③OA=OC,④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.

(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选②③ C.选①③ D.选②④
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
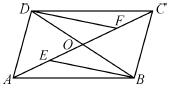
(1)求证:△BOE≌△DOF;
(2)若OD=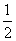 AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com