
 在边长为3 cm和4 cm的长方形中作等腰三角形,其中等腰三角形的两个顶点是长方形的顶点,第三个顶点落在长方形的边上,请作出3种满足上述条件的等腰三角形(全等的等腰三角形视为一种),并分别求出所画三角形的面积.
在边长为3 cm和4 cm的长方形中作等腰三角形,其中等腰三角形的两个顶点是长方形的顶点,第三个顶点落在长方形的边上,请作出3种满足上述条件的等腰三角形(全等的等腰三角形视为一种),并分别求出所画三角形的面积. 分析 分别作BC、AB的中垂线,由中垂线的性质可得等腰三角形,或以点B为圆心,BA长为半径画弧交BC于点F,也可得等腰三角形,最后根据三角形的面积公式可得答案.
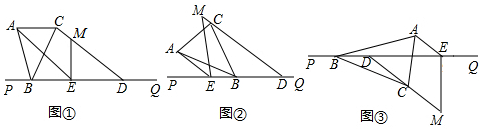
解答 解:如图1,作BC边的中垂线,交AD于P,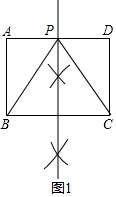
∴PB=PC,即△PBC为等腰三角形,
S△PBC=$\frac{1}{2}$BC×h=$\frac{1}{2}$BC•AB=$\frac{1}{2}$×4×3=6;
如图2,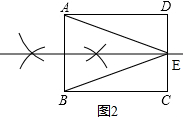
作AB边的中垂线,交CD于E,
∴EA=EB,即△EAB为等腰三角形,
S△EBC=$\frac{1}{2}$AB×h=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×4×3=6;
如图3,以点B为圆心,BA长为半径画弧交BC于点F,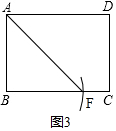
∴BA=BF,即△ABF为等腰三角形,
S△ABF=$\frac{1}{2}$×AB×BF=$\frac{1}{2}$×3×3=4.5.
点评 本题主要考查中垂线的性质及等腰三角形的判定,熟练掌握中垂线的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,点E为BC的中点,若∠B=∠AEF=∠C=90°.连接AF
如图,点E为BC的中点,若∠B=∠AEF=∠C=90°.连接AF查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100(1-x)2=64 | B. | 64(1-x)2=100 | C. | 100(1-2x)=64 | D. | 64(1-2x)=100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
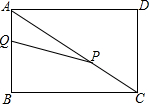 如图,在矩形ABCD中.AB=3cm.Bc=4cm.动点P以2cm/秒的速度从点C出发,沿CA向点A移动.同时动点Q以1cm/秒的速度从点A出发沿AB向点B移动.设P、Q两点移动t秒.
如图,在矩形ABCD中.AB=3cm.Bc=4cm.动点P以2cm/秒的速度从点C出发,沿CA向点A移动.同时动点Q以1cm/秒的速度从点A出发沿AB向点B移动.设P、Q两点移动t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com