Question

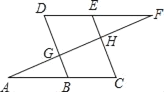
【题目】如图，E在直线DF上，B在直线AC上，若∠AGB＝∠EHF，∠C＝∠D，试判断∠A与∠F的关系，并说明理由．

说明：

因为∠AGB＝∠EHF(已知)

∠AGB＝　 　(依据：　 　)

所以　 　，(等量代换)

所以　 　(依据：　 　)

所以∠C＝　 　，(依据：　 　)

又因为∠C＝∠D，(已知)

所以　 　，(等量代换)

所以DF∥AC(依据：　 　)

所以∠A＝∠F．

Answer 1

【答案】见解析.

【解析】

推出∠EHF=∠DGF，推出BD∥CE，根据平行线的性质推出∠FEH=∠D，根据平行线的判定推出DF∥AC，根据平行线的性质推出即可．

解：因为∠AGB＝∠EHF，∠AGB＝∠DGF(对顶角相等 )

所以∠DGF＝∠EHF，(等量代换)

所以BD∥CE，(同位角相等，两直线平行 )

所以∠C＝∠ABD，(两直线平行，同位角相等)

又因为∠C＝∠D，(已知)

所以∠D＝∠ABD(等量代换)，

所以DF∥AC，(内错角相等，两直线平行)

所以∠A＝∠F．

故答案为：∠DGF，对顶角相等，∠DGF＝∠EHF，同位角相等，两直线平行，∠ABD，两直线平行，同位角相等，∠D＝∠ABD，内错角相等，两直线平行．