
 如图,AB为⊙O的直径,C为AE的中点,连结AE交BC于F点.
如图,AB为⊙O的直径,C为AE的中点,连结AE交BC于F点.| 3 |
 |
| AC |
 |
| CE |
| 3 |
| AC |
| BC |
2
| ||
| 6 |
| ||
| 3 |


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
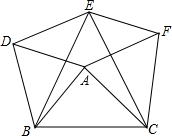 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,查看答案和解析>>
科目:初中数学 来源: 题型:
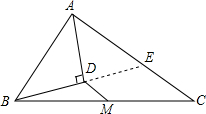 △ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?
如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?查看答案和解析>>
科目:初中数学 来源: 题型:
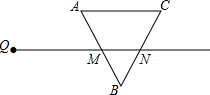 射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com