
【题目】已知:在△ABC中,∠ABC=90°,AB=BC,点D为线段BC上一动点(点D不与点B、C重合),点B关于直线AD的对称点为E,作射线DE,过点C作BC的垂线,交射线DE于点F,连接AE.
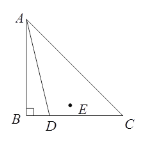
(1)依题意补全图形;
(2)AE与DF的位置关系是 ;
(3)连接AF,小昊通过观察、实验,提出猜想:发现点D 在运动变化的过程中,∠DAF的度数始终保持不变,小昊把这个猜想与同学们进行了交流,经过测量,小昊猜想∠DAF= °,通过讨论,形成了证明该猜想的两种想法:
想法1:过点A作AG⊥CF于点G,构造正方形ABCG,然后可证△AFG≌△AFE……
想法2:过点B作BG∥AF,交直线FC于点G,构造□ABGF,然后可证△AFE≌△BGC……
请你参考上面的想法,帮助小昊完成证明(一种方法即可).
【答案】(1)详见解析;(2)互相垂直;(3)45°,证明详见解析
【解析】
(1)根据题意正确画图;
(2)证明△ABD≌△AED(SSS),可得∠AED=∠B=90°,从而得结论;
(3)想法1:如图2,过点A做AG⊥CF于点G,先证明四边形ABCG是正方形,得AG=AB,∠BAG=90°,再证明Rt△AFG≌Rt△AFE(HL),得∠GAF=∠EAF,根据∠BAG=90°及角的和可得结论;
想法2:如图3,过点B作BG∥AF,交直线FC于点G,证明四边形ABGF是平行四边形,得AF=BG,∠BGC=∠BAF,再证明Rt△AEF≌Rt△BCG (HL),同理根据∠BCG=90°及等量代换,角的和可得结论.
(1)补全图形如下:
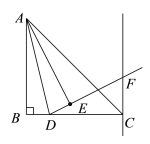
(2)AE与DF的位置关系是:AE⊥DF,
理由是:∵点B关于直线AD的对称点为E,
∴AB=AE,BD=DE,
∵AD=AD,
∴△ABD≌△AED(SSS),
∴∠AED=∠B=90°,
∴AE⊥DF;
故答案为:AE⊥DF;
(3)猜想∠DAF=45°;
想法1:
证明如下:如图2,过点A做AG⊥CF于点G,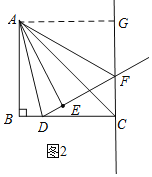
依题意可知:∠B=∠BCG=∠CGA=90°,
∵AB=BC,
∴四边形ABCG是正方形,
∴AG=AB,∠BAG=90°,
∵点B关于直线AD的对称点为E,
∴AB=AE,∠B=∠AED=∠AEF=90°,∠BAD=∠EAD,
∴AG=AE,
∵AF=AF,
∴Rt△AFG≌Rt△AFE(HL),
∴∠GAF=∠EAF,
∵∠BAG=90°,
∴∠BAD+∠EAD+∠EAF+∠GAF=90°,
∴∠EAD+∠EAF=45°.
即∠DAF=45°.
想法2:
证明如下:如图3,过点B作BG∥AF,交直线FC于点G,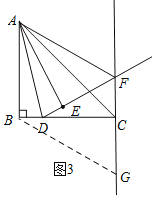
依题意可知:∠ABC=∠BCF=90°,
∴AB∥FG,
∵AF∥BG,
∴四边形ABGF是平行四边形,
∴AF=BG,∠BGC=∠BAF,
∵点B关于直线AD的对称点为E,
∴AB=AE,∠ABC=∠AED=90°,∠BAD=∠EAD,
∵AB=BC,
∴AE=BC,
∴Rt△AEF≌Rt△BCG (HL),
∴∠EAF=∠CBG,
∵∠BCG=90°,
∴∠BGC+∠CBG=90°,
∴∠BAF+∠EAF=90°,
∴∠BAD+∠EAD+∠EAF+∠EAF=90°,
∵∠BAD=∠EAD,
∴∠EAD+∠EAF=45°,
即∠DAF=45°.
故答案为:45.


科目:初中数学 来源: 题型:
【题目】在抗击“新冠肺炎”战役中,某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天的生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.
(1)求甲、乙两条生产线每天的产能各是多少?
(2)若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?
(3)正式开工满负荷生产3天后,通过技术革新,甲生产线的日产能提高了50%,乙生产线的日产能翻了一番.再满负荷生产13天能否完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.
(1)判断CM与⊙O的位置关系,并说明理由;
(2)若∠ECF=2∠A,CM=6,CF=4,求MF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
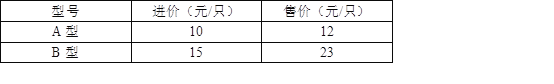
(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药,12周后,记录了两组患者的生理指标![]() 和
和![]() 的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
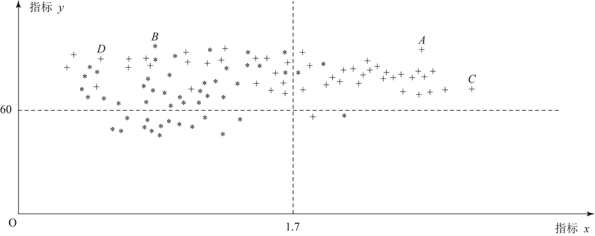
同时记录了服药患者在4周、8周、12周后的指标z的改善情况,并绘制成条形统计图.

根据以上信息,回答下列问题:
(1)从服药的50名患者中随机选出一人,求此人指标![]() 的值大于1.7的概率;
的值大于1.7的概率;
(2)设这100名患者中服药者指标![]() 数据的方差为
数据的方差为![]() ,未服药者指标
,未服药者指标![]() 数据的方差为
数据的方差为![]() ,则
,则![]()
![]() ;(填“>”、“=”或“<” )
;(填“>”、“=”或“<” )
(3)对于指标z的改善情况,下列推断合理的是 .
①服药4周后,超过一半的患者指标z没有改善,说明此药对指标z没有太大作用;
②在服药的12周内,随着服药时间的增长,对指标z的改善效果越来越明显.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新冠肺炎的爆发,市场对口罩的需求量急剧增大.某口罩生产商自二月份以来,--直积极恢复产能,每日口罩生产量![]() (百万个)与天数
(百万个)与天数![]() 且
且![]() 为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数
为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数![]() 呈抛物线型,第
呈抛物线型,第![]() 天市场口罩缺口(需求量与供应量差)就达到
天市场口罩缺口(需求量与供应量差)就达到![]() (百万个),之后若干天,市场口罩需求量不断上升,在第
(百万个),之后若干天,市场口罩需求量不断上升,在第![]() 天需求量达到最高峰
天需求量达到最高峰![]() (百万个).
(百万个).
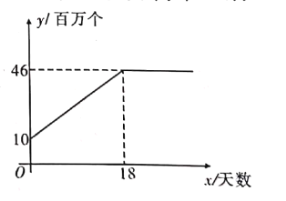
![]() 求出
求出![]() 与
与![]() 的函数解析式;
的函数解析式;
![]() 当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学前夕,某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费125元,购进A品牌文具袋3个和B品牌文具袋各4个共花费90元.
(1)求购进A品牌文具袋和B品牌文具袋的单价;
(2)若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为y元.
①求y关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不超过进货价格的40%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),与y轴交于(0,2),抛物线的对称轴为直线x=1,则下列结论中:①a+c=b;②方程ax2+bx+c=0的解为﹣1和3;③2a+b=0;④c﹣a>2,其中正确的结论有( )
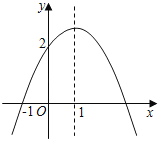
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com