
【题目】在抗击“新冠肺炎”战役中,某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天的生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.
(1)求甲、乙两条生产线每天的产能各是多少?
(2)若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?
(3)正式开工满负荷生产3天后,通过技术革新,甲生产线的日产能提高了50%,乙生产线的日产能翻了一番.再满负荷生产13天能否完成任务?
【答案】(1)甲条生产线每天的产能是40万个,乙条生产线每天的产能是20万个;(2)至少应安排乙生产线生产32天;(3)再满负荷生产13天能完成任务.
【解析】
(1)设乙条生产线每天的产能是x万个,则甲条生产线每天的产能是2x万个,根据题意列出方程即求解可;
(2)设安排乙生产线生产y天,再根据完成这批任务总运行成本不超过40万元列出不等式求解即可;
(3)根据题意求出原来满负荷生产3天和再满负荷生产13天的产能的和,然后与1440万相比即可解答.
解:(1)设乙条生产线每天的产能是x万个,则甲条生产线每天的产能是2x万个,依题意有
![]() ﹣
﹣![]() =2,
=2,
解得x=20,
经检验,x=20是原方程的解,
2x=2×20=40,
故甲条生产线每天的产能是40万个,乙条生产线每天的产能是20万个;
(2)设安排乙生产线生产y天,依题意有
0.5y+1.2×![]() ≤40,
≤40,
解得y≥32.
故至少应安排乙生产线生产32天;
(3)(40+20)×3+[40×(1+50%)+20×2]×13
=180+1300
=1480(万个),
1440万个<1480万个,
故再满负荷生产13天能完成任务.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
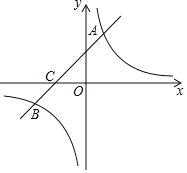
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
⑴求该反比例函数和一次函数的解析式;
⑵在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标;
的坐标;
⑶直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四个命题:①如果一个数的相反数等于它本身,则这个数是0;②一个数的倒数等于它本身,则这个数是1;③一个数的算术平方根等于它本身,则这个数是1或0;④甲、乙两射击运动员分别射击10次,他们射击成绩的方差分别为![]() =5,
=5,![]() =2,这一过程中乙发挥比甲更稳定.⑤点M(a,b),N(c,d)都在反比例函数y=
=2,这一过程中乙发挥比甲更稳定.⑤点M(a,b),N(c,d)都在反比例函数y=![]() 的图象上.若a<c,则b>d.其中真命题有( )个.
的图象上.若a<c,则b>d.其中真命题有( )个.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
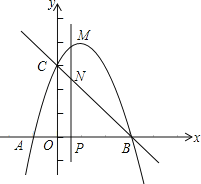
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,求线段MN的最大值;
(3)是否存在点P,使得以点C、O、M、N为顶点的四边形是平行四边形?若存在,请直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
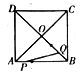
【题目】如图,四边形ABCD是正方形,![]() ,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是
,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是![]() ,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,
,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,![]() 的面积为y,则y关于x的函数图象大致为( )
的面积为y,则y关于x的函数图象大致为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是某火车站候车室前的自动扶梯,长为30m,坡角为37°,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度.(结果精确到0.1m)(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
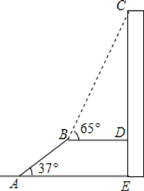
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠ABC=90°,AB=BC,点D为线段BC上一动点(点D不与点B、C重合),点B关于直线AD的对称点为E,作射线DE,过点C作BC的垂线,交射线DE于点F,连接AE.
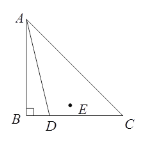
(1)依题意补全图形;
(2)AE与DF的位置关系是 ;
(3)连接AF,小昊通过观察、实验,提出猜想:发现点D 在运动变化的过程中,∠DAF的度数始终保持不变,小昊把这个猜想与同学们进行了交流,经过测量,小昊猜想∠DAF= °,通过讨论,形成了证明该猜想的两种想法:
想法1:过点A作AG⊥CF于点G,构造正方形ABCG,然后可证△AFG≌△AFE……
想法2:过点B作BG∥AF,交直线FC于点G,构造□ABGF,然后可证△AFE≌△BGC……
请你参考上面的想法,帮助小昊完成证明(一种方法即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com