
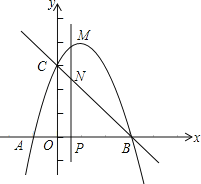
����Ŀ����ͼ��������y����x2+bx+c��x�ύ��A����1��0����B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��0��3������ֱ��BC������P��x�����˶�������P��PM��x�ᣬ���������ڵ�M����ֱ��BC�ڵ�N�����P�ĺ�����Ϊm��
��1���������ߵĽ���ʽ��
��2������P���߶�OB���˶�ʱ�����߶�MN�����ֵ��
��3���Ƿ���ڵ�P��ʹ���Ե�C��O��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д��m��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1)y����x2+2x+3��(2)�߶�MN���ֵΪ![]() ��(3)���ڵ�P��ʹ���Ե�C��O��M��NΪ������ı�����ƽ���ı��Σ���ʱm��ֵΪ
��(3)���ڵ�P��ʹ���Ե�C��O��M��NΪ������ı�����ƽ���ı��Σ���ʱm��ֵΪ![]() ��
��![]() ��
��
��������
��1�����ݵ�A��C�����꣬���ô���ϵ����������������ߵĽ���ʽ��
��2���ɶ��κ���ͼ���ϵ�������������ҳ���B�����꣬���ݵ�B��C�����꣬���ô���ϵ���������ֱ��BC�Ľ���ʽ�����P������Ϊ��m��0����0��m��3������M������Ϊ��m����m2+2m+3������N������Ϊ��m����m+3�����ɴ˼��ɵó�MN����m2+3m�������䷽����������߶�MN�����ֵ��
��3������ƽ���ı��ε����ʿɵó�MN��OC����m��0��m��3�Լ�0��m��3������������ɵó�����m��һԪ���η��̣���֮���ɵó����ۣ�
(1)��A(��1��0)��C(0��3)����y����x2+bx+c��
![]() ����ã�
����ã�![]() ,
,
�������ߵĽ���ʽΪy����x2+2x+3��
(2)��y����x2+2x+3��0ʱ��x1����1��x2��3��
���B������Ϊ(3��0)��
��ֱ��BC�Ľ���ʽΪy��kx+b(k��0)��
��B(3��0)��C(0��3)����y��kx+b��
![]() ,����ã�
,����ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪy����x+3��
���P������Ϊ(m��0)(0��m��3)����M������Ϊ(m����m2+2m+3)��
��N������Ϊ(m����m+3)��
��MN����m2+2m+3��(��m+3)����m2+3m����(m��![]() )2+
)2+![]() ��
��
�൱m��![]() ���߶�MNȡ���ֵ�����ֵΪ
���߶�MNȡ���ֵ�����ֵΪ![]() ��
��
(3)��MN��CO��
�൱MN��COʱ���Ե�C��O��M��NΪ������ı�����ƽ���ı��Σ�
�ߵ�O(0��0)��C(0��3)��
��OC��3��
��|��m2+3m|��3��
��m��0��m��3ʱ����m2��3m��3��
��ã�m1��![]() ��m2��
��m2��![]() ��
��
��0��m��3ʱ���Щ�m2+3m��3��
�ߡ���(��3)2��4��1��3����3��0��
���ʱ�����⣮
�������������ڵ�P��ʹ���Ե�C��O��M��NΪ������ı�����ƽ���ı��Σ���ʱm��ֵΪ![]() ��
��![]() ��
��


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����龳
��ѧ����ϣ���ʦ��ͬѧ���ԡ������ε���ת��Ϊ���չ��ѧ���![]() ��
��![]() ������ȫ�ȵ�ֱ��������ֽƬ������
������ȫ�ȵ�ֱ��������ֽƬ������![]() ��
��![]() ��
��![]() ��
��
�������
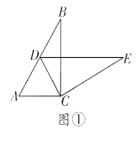
��1����ͼ�٣��ǻ�С�齫![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�����ֵ���
˳ʱ����ת�����ֵ���![]() ǡ������
ǡ������![]() ����ʱ��
����ʱ��![]() �����������֤��������ۣ�
�����������֤��������ۣ�
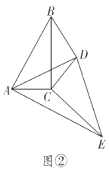
��2������С�����ǻ�С��Ļ����ϼ���̽��������![]() ����
����![]() C�Ƶ�
C�Ƶ�![]() ������ת����ͼ����ʾ��λ��ʱ���������
������ת����ͼ����ʾ��λ��ʱ���������![]() �������������֤��һ�����Ƿ���ȷ����˵�����ɣ�
�������������֤��һ�����Ƿ���ȷ����˵�����ɣ�
̽������
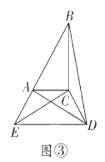
��3����ͼ�ۣ��ڷ�С����ǰ����С��������£�������ת![]() ����
����![]() ���㹲��ʱ����
���㹲��ʱ����![]() �ij���
�ij���
��4����ͼ�ٵĻ����ϣ�д��һ���߳���Ϊ![]() �������Σ���������ĸ����
�������Σ���������ĸ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
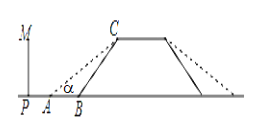
����Ŀ��ij�ص�һ������������ͼ��ʾ�����Ÿ�Ϊ6�ף�����BC���¶�Ϊ1��1��Ϊ�˷��������Ƴ������ţ��йز��ž��������¶ȣ�ʹ��������¶�Ϊ1��![]() ��
��
��1������������½ǡ�CAB�Ķ�����
��2��ԭ���ŵײ���ǰ��8�״���PB�ij������Ļ�ǽPM�Ƿ���Ҫ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ����������ʼ���ڹ�Ԫ1049�꣨���λʵvԪ�꣩���ǹ����ص㱣������֮һ����900�����У����������ε��𡢴�硢ˮ����ΡȻ���������С����µ�һ����֮�ƣ���ͼ��С��������һ���ˮƽ����һ��̨�ĵײ�A���������P������Ϊ45�㣬�ߵ�̨����B�����ֲ������P������Ϊ38.7�㣬��̨֪���ܸ߶�BCΪ3�ף��ܳ���ACΪ10�ף����������ĸ߶ȣ��������ȷ��1�ף��ο����ݣ�sin38.7���0.63��cos38.7���0.78��tan38.7���0.80��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����̩ɽ�Ļ���ijУ�ٰ�����̩ɽʫ�Ĵ�����������������ȡ����ѧ���ı����ɼ������ݳɼ����ɼ�������50�֣������������µ�ͳ��ͼ��������������
��� | ���� | ���� |
��1�� | 90��x��100 | 8 |
��2�� | 80��x��90 | a |
��3�� | 70��x��80 | 10 |
��4�� | 60��x��70 | b |
��5�� | 50��x��60 | 3 |
�����������Ϣ������������⣺

��1�����a��b��ֵ��
��2����������ͳ��ͼ������5������������Բ�ĽǵĶ�����
��3������У����1800��ѧ������ô�ɼ�����80�ֵĹ��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڿ������¹ڷ��ס�ս���У�ij��˾�ӵ�ת������1440���ҽ�÷������ֲ������һ����Ҫ��������ʱ�����˼ס���������ˮ�����ߣ��Բ�ʱ��������ÿ��IJ��ܣ�ÿ������������������������ߵ�2����������80������ױ���������2�죮
��1����ס�������������ÿ��IJ��ܸ��Ƕ��٣�
��2�����ס�������������ÿ������гɱ��ֱ���1.2��Ԫ��0.5��Ԫ��Ҫʹ����������������гɱ�������40��Ԫ��������Ӧ���������������������죿
��3����ʽ��������������3���ͨ���������£��������ߵ��ղ��������50%���������ߵ��ղ��ܷ���һ����������������13���ܷ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=kx+4����κ���y=ax2+c��ͼ���һ����������Ϊ��1,2������һ�������Ǹö��κ���ͼ��Ķ���
��1����k��a��c��ֵ��
��2������A��0��m����0��m��4���Ҵ�ֱ��y���ֱ������κ���y=ax2+c��ͼ���ཻ��B��C���㣬��OΪ����ԭ�㣬��W=OA2+BC2����W����m�ĺ�������ʽ������W����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ƽ���ı���OABC�ĶԽ��߽��ڵ�D��˫����![]() ����C��D ���㣬˫����
����C��D ���㣬˫����![]() ������B����ƽ���ı���OABC�����Ϊ�� ��
������B����ƽ���ı���OABC�����Ϊ�� ��
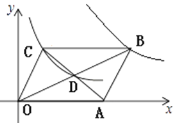
A.4B.6C.7D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С�Ź���100ֻ�����ͺŵ��ľ߽������ۣ�����ۺ��ۼ�֮��Ĺ�ϵ���±���
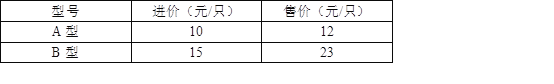
��1��С����ν�����ʹ������ǡ��Ϊ1300Ԫ��
��2��Ҫʹ�����ľ�����������������������������۸��40%�������С�����һ�������������������������������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com