
【题目】如图,在每个小正方形的边长为1的网格中,![]() ,
,![]() ,
,![]() 为格点,
为格点,![]() 为小正方形边的中点.
为小正方形边的中点.
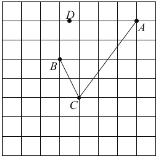
(1)![]() 的长等于_________;
的长等于_________;
(2)点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,当
上的动点,当![]() 取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段
取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段![]() ,
,![]() ,并简要说明点
,并简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明).
的位置是如何找到的(不要求证明).
【答案】(1)5;(2)见解析
【解析】
(1)直接利用勾股定理计算可得;
(2)令BC与网格交于P,再分别取网格线中点G和H,连接,与AC交于Q,从而可得.
解:(1)由图可得:
AC=![]() ,
,
故答案为:5;
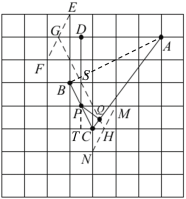
(2)如图,![]() 与网格线相交,得点
与网格线相交,得点![]() ;取格点
;取格点![]() ,
,![]() ,连接
,连接![]() ,与网格线相交,得点
,与网格线相交,得点![]() ,取格点
,取格点![]() ,
,![]() ,连接
,连接![]() ,与网格线相交,得点
,与网格线相交,得点![]() ,连接
,连接![]() ,与
,与![]() 相交,得点
相交,得点![]() .连接
.连接![]() ,
,![]() .线段
.线段![]() ,
,![]() 即为所求.
即为所求.
如图,延长DP,交网格线于点T,连接AB,GH与DP交于点S,
由计算可得:AB=![]() ,BC=
,BC=![]() ,AC=5,
,AC=5,
∴△ABC为直角三角形,∠ABC=90°,
∴tan∠ACB=2,
∵tan∠BCT=PT:TC=2,
∴∠ACB=∠BCT,即BC平分∠ACT,
根据画图可知:GH∥BC,
∴∠ACB=∠CQH,∠BCT=∠GHC,
∵∠BCT=∠BCA,
∴∠CQH=∠GHC,
∴CQ=CH,
由题意可得:BS=CH,
∴BS=CQ,
又∵BP=CP,∠PBS=∠PCQ,
∴△BPS≌△CPQ,
∴∠PSB=∠PHC=90°,即PQ⊥AC,
∴PD+PQ的最小值即为PD+PT,
∴所画图形符合要求.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是![]() 上一点,∠ADC=∠G.
上一点,∠ADC=∠G.
(1)求证:∠1=∠2;
(2)点C关于DG的对称点为F,连结CF,当点F落在直径AB上时,CF=10,tan∠1=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
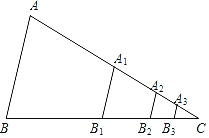
【题目】如图,△ABC的面积为4,分别取AC,BC两边的中点A1,B1,记△A1B1C的面积为S1;再分别取A1C,B1C的中点A2,B2,记△A2B2C的面积为S2,再分别取A2C,B2C的中点A3,B3,记△A3B3C的面积为S3;则S3的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
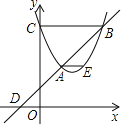
【题目】如图,在平面直角坐标系中,抛物线y=x2﹣mx+4与y轴交于点C,过点C作x轴的平行线交抛物线于点B,点A在抛物线上,点B关于点A的对称点D恰好落在x轴负半轴上,过点A作x轴的平行线交抛物线于点E.若点A、D的横坐标分别为1、﹣1,则线段AE与线段CB的长度和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= (n为常数).
(n为常数).
(1)当n=1时,
①点P(﹣3,m)在此函数图象上,求m的值.
②当﹣4≤x≤3时,求此函数的最大值和最小值.
(2)当x<n时,若此函数的图象与坐标轴只有两个交点,求n的取值范围.
(3)若n>0,当此函数的图象与以A(0,3)、B(5,﹣2)、C(﹣5,﹣2)、D(﹣5,3)为顶点的四边形的边有且只有四个公共点时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
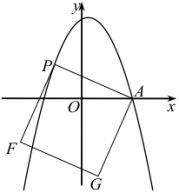
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
(1)求抛物线的解析式;
(2)![]() 为抛物线上的一个动点,点
为抛物线上的一个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() .当点
.当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
(3)![]()
![]() 是抛物线上一动点,连接
是抛物线上一动点,连接![]() ,以
,以![]() 为边作图示一侧的正方形
为边作图示一侧的正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小与位置也随之改变,当顶点
的运动,正方形的大小与位置也随之改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,求对应的
轴上时,求对应的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
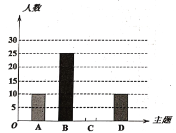
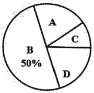
【题目】某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“A”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家“垃圾分类进校园”的号召,某校准备购买新的分类垃圾箱进行更换,已知购买5个A类垃圾箱和4个B类垃圾箱需花费1600元,购买3个A类垃圾箱的费用恰好等于购买4个B类垃圾箱的费用.
(1)求购买一个A类垃圾箱和一个B类垃圾箱各需多少元;
(2)该校计划用不超过9000元的经费购买A类和B类垃圾箱共50个,其中A类垃圾箱的数量不低于25个,则本次可以选择的方案有几种;
(3)在(2)的条件下哪种方案的费用最低,最低费用是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交点C,抛物线
与x轴交于点A,与y轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
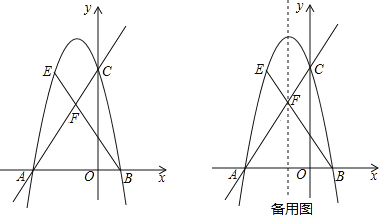
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求
时,求![]() 的值.
的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com