
【题目】已知抛物线![]() 的顶点
的顶点![]() 在定直线
在定直线![]() 上.
上.
(1)求![]() 点的坐标(用含
点的坐标(用含![]() 的式子表示);
的式子表示);
(2)求证:不论![]() 为何值,抛物线与定直线
为何值,抛物线与定直线![]() 的两交点间的距离
的两交点间的距离![]() 恒为定值;
恒为定值;
(3)当![]() 的顶点
的顶点![]() 在
在![]() 轴上,且与
轴上,且与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧)时,在
点左侧)时,在![]() 上是否存在两点
上是否存在两点![]() 、
、![]() ,设
,设![]() 交线段
交线段![]() 于
于![]() 点,使
点,使![]() ,且直线
,且直线![]() 将
将![]() 的面积分成
的面积分成![]() 的两部分?若存在,求出直线
的两部分?若存在,求出直线![]() 的解析式;若不存在,请说明理由.
的解析式;若不存在,请说明理由.
【答案】(1)C(-2m,-4m-3);(2)见解析;(3)存在,直线MN的解析式为:y=![]() x+3-2
x+3-2![]() 或y=
或y=![]() x+3-2
x+3-2![]() .
.
【解析】
(1)可用配方法将抛物线的解析式配成顶点式,从而可得出结果;
(2)设顶点坐标为(x,y),从而可用含m的代数式表示x、y,消去m,就可得到x与y的关系,得出定直线l的解析式,将直线l的解析式与抛物线的解析式联立,消去y,求出x,就可得到两交点的横坐标,将横坐标代入直线l的解析式进而可得出两个交点的坐标,然后运用两点之间的距离公式就可解决问题;
(3)先得出C1的解析式,求出A,B,C的坐标,再进一步得出∠ACB=60°,所以MN∥BC,从而根据直线BC的解析式可设MN的解析式为y=![]() x+m.由直线MN将△ABC的面积分成
x+m.由直线MN将△ABC的面积分成![]() 两部分,设MN与x轴交于点T,可分为以下两种情况:①当S△APT:S四边形PTBC=1:2时,则S△APT=
两部分,设MN与x轴交于点T,可分为以下两种情况:①当S△APT:S四边形PTBC=1:2时,则S△APT=![]() S△ABC;当S△APT:S四边形PTBC=2:1时,则S△APT=
S△ABC;当S△APT:S四边形PTBC=2:1时,则S△APT=![]() S△ABC,再根据相似三角形的性质可求出AT的长,从而可得出点T的坐标,代入直线MN的解析式可求出m的值,即可得出结果.
S△ABC,再根据相似三角形的性质可求出AT的长,从而可得出点T的坐标,代入直线MN的解析式可求出m的值,即可得出结果.
解:(1)∵y=x2+4mx+4m2-4m-3=(x+2m)2-4m-3,
∴抛物线的顶点C的坐标为(-2m,-4m-3);
(2)设抛物线的顶点坐标为(x,y),
则有x=-2m①,y=-4m-3②,
由①②消去m得,y=2x-3,
∴定直线l的解析式为y=2x-3.
联立抛物线与直线l的解析式得,
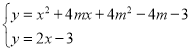 ,消去y整理得,x2+(4m-2)x+4m2-4m=0,
,消去y整理得,x2+(4m-2)x+4m2-4m=0,
∴(x+2m)(x+2m-2)=0,∴x1=-2m,x2=2-2m,
∴抛物线与定直线l的两交点坐标为(-2m,-4m-3),(2-2m,1-4m),
∴d=![]() =
=![]() .
.
故不论![]() 为何值,抛物线与定直线
为何值,抛物线与定直线![]() 的两交点间的距离
的两交点间的距离![]() 恒为定值;
恒为定值;
(3)存在.∵抛物线的顶点在y轴上,∴-2m=0,即m=0.
∴C1的解析式为y=x2-3,
∴A(-![]() ,0),B(
,0),B(![]() ,0),C(0,-3),
,0),C(0,-3),
∴BO=AO=![]() ,OC=3,∴AB=2
,OC=3,∴AB=2![]() ,tan∠ACO=
,tan∠ACO=![]() ,
,
∴∠ACO=30°,同理可得∠BCO=30°,
∴∠APN=2∠ACO=60°,∴∠APN=∠ACB=60°,
∴MN∥BC,
设直线BC的解析式为y=kx+b,则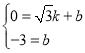 ,得k=
,得k=![]() ,
,
∴设直线MN的解析式为y=![]() x+m,设MN与x轴交于点T,
x+m,设MN与x轴交于点T,
情况1:如图①,当S△APT:S四边形PTBC=1:2时,则S△APT=![]() S△ABC,
S△ABC,
又PT∥BC,∴△APT∽△ACB,
∴![]() ,∴AT=
,∴AT=![]() =2,∴OT=2-
=2,∴OT=2-![]() ,
,
∴点T的坐标为(2-![]() ,0).
,0).
将点T的坐标代入y=![]() x+m得,m=3-2
x+m得,m=3-2![]() ,
,
∴直线MN的解析式为y=![]() x+3-2
x+3-2![]() .
.
情况2:如图②,当S△APT:S四边形PTBC=2:1时,则S△APT=![]() S△ABC,
S△ABC,
∴![]() ,∴AT=
,∴AT=![]() =2
=2![]() ,∴OT=2
,∴OT=2![]() -
-![]() ,
,
∴点T的坐标为(2![]() -
-![]() ,0).
,0).
将点T的坐标代入y=![]() x+m得,m=3-2
x+m得,m=3-2![]() ,
,
∴直线MN的解析式为y=![]() x+3-2
x+3-2![]() .
.
综上所述,直线MN的解析式为:y=![]() x+3-2
x+3-2![]() 或y=
或y=![]() x+3-2
x+3-2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图AB是圆O的直径,射线AM⊥AB于点A.点D在AM上,连接OD交圆O于点E,过点D作DC=DA.交圆O于点C(A,C不重合),连接BC,CE.
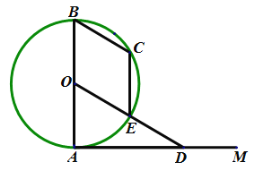
(1)求证:CD是圆O的切线;
(2)若四边形OECB是菱形,圆O的直径AB=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() ,有下列结论:①其图象与x轴一定相交;②若
,有下列结论:①其图象与x轴一定相交;②若![]() ,函数在
,函数在![]() 时,y随x的增大而减小;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中所有正确的结论是___.(填写正确结论的序号)
时,y随x的增大而减小;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中所有正确的结论是___.(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
(1)试确定这两函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=1,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆交BC于D,过D作⊙O的切线EF交AC于E,交AB延长线于F.
(1)求证:DE⊥AC.
(2)若BD=2![]() ,tan∠CDE=
,tan∠CDE=![]() ,求BF的长.
,求BF的长.
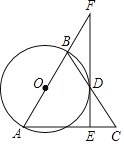
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了检验甲、乙两个车间生产的同一款产品的质量情况,进行了抽样调查,请补充完整.
收集数据 从甲、乙两个车间各随机抽取20个样品,进行了检测,检测结果(单位:mm)如下:
甲车间 | 168 | 175 | 180 | 185 | 172 | 189 | 185 | 182 | 185 | 174 |
192 | 180 | 185 | 178 | 173 | 185 | 169 | 187 | 176 | 180 | |
乙车间 | 186 | 180 | 189 | 183 | 176 | 173 | 178 | 167 | 180 | 175 |
178 | 182 | 180 | 179 | 185 | 180 | 184 | 182 | 180 | 183 |
整理、描述数据 按如下分段整理、描述这两组样本数据:
165.5-170.5 | 170.5-175.5 | 175.5-180.5 | 180.5-185.5 | 185.5-190.5 | 190.5-195.5 | |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 |
(说明:尺寸范围为176mm~190mm的产品为合格)
分析数据 两组样本数据的平均数、众数、中位数、方差如下表所示:
平均数 | 众数 | 中位数 | 方差 | |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
得出结论
(1)补全上列表格;
(2)若乙车间生产1000个该款产品,估计其中合格产品约有 个;
(3)可以推断出 车间生产的该款产品更好,理由为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com