
����Ŀ����ͼ����ˮƽ�����A����һ������������з��������������·����һ�������ߣ��ڵ��������ΪB��������ֱ��AB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ��ǵ�Բ����Ͱ����ͼ����������Ͱ�ڣ���֪AB=4�ף�AC=3�ף�����������߶�OM=5�ף�Բ����Ͱ��ֱ��CDΪ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ���
��1����ͼ������ֱ������ϵ����������ߵĽ���ʽ��
��2�������ֱ�ڷ�7��Բ����Ͱʱ�������ܲ�������Ͱ�ڣ�
��3������ֱ�ڷ�Բ����Ͱ������ٸ�ʱ�������������Ͱ�ڣ�
���𰸡�
��1��
�⣺M��0��5����B��2��0����C��1��0����D�� ![]() ��0����
��0����
�������ߵĽ���ʽΪy=ax2+k��
�������߹���M�͵�B��
��k=5�� ![]() ��
��
�������߽���ʽΪ ![]() ��
��
��2��
�⣺��x=1ʱ��y= ![]() ����x=
����x= ![]() ʱ��y=
ʱ��y= ![]() ��
��
��P��1�� ![]() ����Q��
����Q�� ![]() ��
�� ![]() ��
��
����ֱ�ڷ�7��Բ����Ͱʱ��Ͱ��= ![]() ��7=2.1��
��7=2.1��
��2.1�� ![]() ��2.1��
��2.1�� ![]() ��
��
������������Ͱ�ڣ�
��3��
�⣺����ֱ�ڷ�Բ����Ͱm��ʱ�����������Ͱ�ڣ�
�����⣬�ã� ![]() ��0.3m��
��0.3m�� ![]() ��
��
��ã� ![]() ��m��
��m�� ![]() ��
��
��m������
��m��ֵΪ8��9��10��11��12��
�൱��ֱ�ڷ�Բ����Ͱ����12��ʱ�������������Ͱ�ڣ�
����������1���������ߵĶԳ���Ϊy�ᣬˮƽ����Ϊx�ᣬ����ƽ��ֱ������ϵ�������ʽ�������֪ȷ���������ϵ�����꣬�������ʽȷ�������ߵĽ���ʽ����2�����õ�x=1ʱ��y= ![]() ����x=1.5 ʱ��y=
����x=1.5 ʱ��y= ![]() ���ó�����ֱ�ڷ�5��Բ����Ͱʱ���ó�Ͱ�߽����Ƚϣ����ɵó��𰸣���3����ԲͰ��ֱ�������ԲͰ����Ե�������ֵ��ȷ��m�ķ�Χ������mΪ���������ó�m��ֵ�����ɵõ��������������Ͱ��ʱ����ֱ�ڷ�Բ����Ͱ������
���ó�����ֱ�ڷ�5��Բ����Ͱʱ���ó�Ͱ�߽����Ƚϣ����ɵó��𰸣���3����ԲͰ��ֱ�������ԲͰ����Ե�������ֵ��ȷ��m�ķ�Χ������mΪ���������ó�m��ֵ�����ɵõ��������������Ͱ��ʱ����ֱ�ڷ�Բ����Ͱ������
�����㾫����������Ĺؼ�����������κ�����ͼ������֪ʶ�����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣬�Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߲�Ʒ�ĸ���ֵ��ij��˾�ƻ����з�������1200���²�Ʒ���о��ӹ�����Ͷ���г������мס��������������߱��ӹ���������˾�ɳ������Ա�ֱ������������˽���������������Ϣ��
��Ϣһ�����������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ����10�죻
��Ϣ�����ҹ���ÿ��ӹ��������Ǽ���ÿ��ӹ�������1.5����
����������Ϣ����ס�����������ÿ��ֱ��ܼӹ����ټ��²�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ĺ�����װ��2ö��ɫ�����Ӻ�1ö��ɫ�����ӣ�ÿö���ӳ�����ɫ���������ͬ���Ӻ����������һö���ӣ�������ɫ��Żز����ȣ��ٴӺ������������һö���ӣ�������ɫ���û���״ͼ�����б����ķ�����������������������ɫ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����BAC��50�㣬��BAC��ƽ������AB���д��߽��ڵ�O����C��EF�۵������O�غϣ����CEO�Ķ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x=��1�������ĸ����ۣ�������ȷ�����ǣ� ��
A.b2��4ac
B.2a+b=0
C.a+b+c��0
D.����B�� ![]() ��y1����C��
��y1����C�� ![]() ��y2��Ϊ����ͼ���ϵ����㣬��y1��y2
��y2��Ϊ����ͼ���ϵ����㣬��y1��y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ADF����BCE�У���A=��B����D��E��F��C��ͬ��ֱ���ϣ�������������ϵʽ����AD=BC����DE=CF����BE��AF��

��1����������������ϵʽ��Ϊ��������һ����Ϊ���ۣ�д����������Ϊ��ȷ�����⣮�������д��������д��ʽ���磺����١�������ô�ۣ�
��2��ѡ��1������д����һ�����⣬˵������ȷ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ������A����1��y1����B����6��y2������ͼ���ϵ����㣬��y1��y2�Ĵ�С��ϵ�ǣ� ��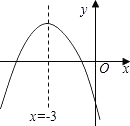
A.y1��y2
B.y1=y2
C.y1��y2
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��ʾ AD��AE�ֱ�����ABC�����ߡ��ߣ���AB=5cm��AC=3cm��,����ABD����ACD���ܳ�֮��Ϊ_________����ABD����ACD�������ϵΪ_________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ε��ܳ�Ϊ38����һ���߳�Ϊa���ڶ����߱ȵ�һ���ߵ�2����3��
��1����ʾ�������ߣ�
��2����������Ϊ���������Σ���a��ֵ��
��3����aΪ�����������������Ƿ�Ϊֱ�������Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com