练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系xOy中，直线y=﹣3x+m与双曲线y= 相交于点A（m，2）．
    （1）求双曲线y= 的表达式；
    （2）过动点P（n，0）且垂直于x轴的直线与直线y=﹣3x+m及双曲线y= 的交点分别为B和C，当点B位于点C下方时，求出n的取值范围．

    【答案】
    （1）解：）∵点A（m，2）在直线y=﹣3x+m上，

    ∴2=﹣3m+m，

    解得：m=﹣1，

    ∴A（﹣1，2）．

    ∵点A在双曲线 上，

    ∴ ，k=﹣2，

    ∴双曲线的表达式为y=﹣ ．


    （2）解：令y=﹣3x﹣1=﹣ ，

    解得：x1=﹣1，x2= ．

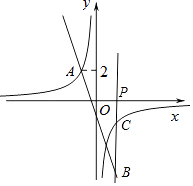
    观察函数图象可知：当﹣1＜n＜0或n＞ 时，反比例函数图象在一次函数图象的上方，即点B位于点C下方，

    ∴当点B位于点C下方时，n的取值范围为﹣1＜n＜0或n＞ ．


    【解析】（1）由点A的坐标利用一次函数图象上点的坐标特征即可求出m值，进而可得出点A的坐标，再由点A的坐标利用待定系数法即可求出双曲线的表达式；（2）令﹣3x﹣1=﹣ ，可求出两函数图象交点的横坐标，再根据两函数图象的上下位置关系即可得出当点B位于点C下方时，n的取值范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（　　）

    A. 4B. 3C. 2D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

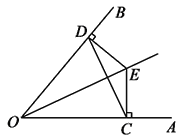
    【题目】如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．

    （1）求证：ED=EC；

    （2）求证：∠ECD=∠EDC；

    （3）求证：OE垂直平分CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，抛物线y=mx2﹣2m2x+2交y轴于A点，交直线x=4于B点．
    （1）抛物线的对称轴为x=（用含m的代数式表示）；
    （2）若AB∥x轴，求抛物线的表达式；
    （3）记抛物线在A，B之间的部分为图象G（包含A，B两点），若对于图象G上任意一点P（xp ， yp），yp≤2，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且AB=FC，E为AD上一点，EC交AF于点G，EA=EG． 求证：ED=EC．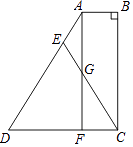

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】八(2)班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表(10分制)：

    甲

    7

    8

    9

    7

    10

    10

    9

    10

    10

    10

    乙

    10

    8

    7

    9

    8

    10

    10

    9

    10

    9

    (1)甲队成绩的中位数是 分，乙队成绩的众数是 分；

    (2)计算乙队的平均成绩和方差；

    (3)已知甲队成绩的方差是1.4，则成绩较为整齐的是 队．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下面例题的解法，然后解答问题：

    例：若多项式2x3-x2+m分解因式的结果中有因式2x+1，求实数m的值.

    解：设2x3-x2+m=(2x+1)·A(A为整式).

    若2x3-x2+m=(2x+1)·A=0，则2x+1=0或A=0.

    由2x+1=0，解得x=-.

    ∴x=-是方程2x3-x2+m=0的解.

    ∴2×(-)3-(-)2+m=0，即--+m=0.

    ∴m=.

    请你模仿上面的方法尝试解决下面的问题：

    若多项式x4+mx3+nx-16分解因式的结果中有因式(x-1)和(x-2)，求实数m，n的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

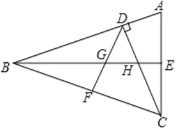
    【题目】如图，CD 和 BE 是△ABC 的两条高，∠BCD＝45°，BF＝FC，BE与 DF、DC分别交于点 G、H，∠ACD＝∠CBE．

    (1)证明：AB＝BC；

    (2)判断 BH 与 AE 之间的数量关系，并证明你的结论；

    (3)结合已知条件，观察图形，你还能发现什么结论？请写出两个（不与前面结论相同）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形，并将添加的全等条件标注在图上．

    请你参考这个作全等三角形的方法，解答下列问题：

    （1）如图2，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC和∠BCA的平分线，AD、CE相交于点F，求∠EFA的度数；

    （2）在（1）的条件下，请判断FE与FD之间的数量关系，并说明理由；

    （3）如图3，在△ABC中，如果∠ACB不是直角，而（ 1 ）中的其他条件不变，试问在（2）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

    查看答案和解析>>

    同步练习册答案