
【题目】如图,CD 和 BE 是△ABC 的两条高,∠BCD=45°,BF=FC,BE与 DF、DC分别交于点 G、H,∠ACD=∠CBE.
(1)证明:AB=BC;
(2)判断 BH 与 AE 之间的数量关系,并证明你的结论;
(3)结合已知条件,观察图形,你还能发现什么结论?请写出两个(不与前面结论相同).
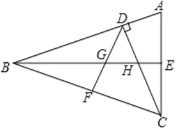
【答案】(1)见解析;(2)BH=2AE;(3)DF 平分∠BDC,DF⊥BC,DG=DH 等.
【解析】
(1)由CD和BE是ΔABC的两条高,于是得到∠A=∠ACD+∠A=90![]() ,于是得到∠ABE=∠ACD,因为∠ACD=∠CBE,折叠∠ABE=∠CBE,通过ΔBAE≌ΔBCE,根据全等三角形的性质得到BA=BC,于是得到结论;
,于是得到∠ABE=∠ACD,因为∠ACD=∠CBE,折叠∠ABE=∠CBE,通过ΔBAE≌ΔBCE,根据全等三角形的性质得到BA=BC,于是得到结论;
(2)根据等腰直角三角形的性质得到BD=DC证得ΔBDH≌ΔCDA,根据全等三角形的性质得到BH=AC,根据直角三角形的性质得到AC=2AE,BH=2AE,即可得到结论;
(3)根据等腰直角三角形的性质,即可得到DF平分∠BDC,DF⊥BC.根据等角的余角相等,即可得出DG=DH,
解: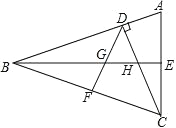
(1)∵CD 和 BE 是△ABC 的两条高,
∴∠ACD+∠A=90°=∠ABE+∠A,
∴∠ABE=∠ACD,
∵∠ACD=∠CBE,
∴∠ABE=∠CBE,
∵∠BEA=∠BEC=90°,
在△BAE 与△BCE 中,
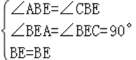
∴△BAE≌△BCE(AAS),
∴BA=BC;
(2)BH=2AE,理由:
∵∠BDC=90°,∠BCD=45°,
∴BD=DC,
∵∠BDH=∠CDA=90°, 在△BDH 与△CDA 中,
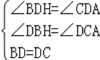
∴△BDH≌△CDA(AAS),
∴BH=AC,
∵BE⊥AC,
∴AC=2AE,
∴BH=2AE;
(3)存在:DF 平分∠BDC,DF⊥BC,DG=DH 等.理由:
∵△BCD 是等腰直角三角形,BF=CF,
∴DF 平分∠BDC,DF⊥BC;
∵∠ABE=∠CBE,∠BDH=∠BFG=90°,
∴∠BHD=∠BGF=∠DGH,
∴DG=DH.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】下面是“作三角形一边中线”的尺规作图过程. 已知:△ABC(如图1),求作:BC边上的中线AD.
作法:如图2,
(i)分别以点B,C为圆心,AC,AB长为半径作弧,两弧相交于P点;
(ii)作直线AP,AP与BC交于D点.
所以线段AD就是所求作的中线.
请回答:该作图的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣3x+m与双曲线y= ![]() 相交于点A(m,2).
相交于点A(m,2). 
(1)求双曲线y= ![]() 的表达式;
的表达式;
(2)过动点P(n,0)且垂直于x轴的直线与直线y=﹣3x+m及双曲线y= ![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,BO 平分∠ABC,CO 平分∠ACB,MN 经过点 O,与 AB、AC 相交于点 M、N,且 MN∥BC,那么下列说法中:①∠MOB=∠MBO②△AMN 的周长等于 AB+AC;③∠A=2∠BOC﹣180°;④连接 AO,则![]() :
:![]() :
:![]() =AB:AC:BC;正确的有( )
=AB:AC:BC;正确的有( )
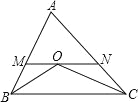
A. ①②④ B. ①②③ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+2m﹣1(m≠0)与平行于x轴的一条直线交于A,B两点. 
(1)求抛物线的对称轴;
(2)如果点A的坐标是(﹣1,﹣2),求点B的坐标;
(3)抛物线的对称轴交直线AB于点C,如果直线AB与y轴交点的纵坐标为﹣1,且抛物线顶点D到点C的距离大于2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园的绿化工程,甲、乙两队单独完成这项工作所需的时间比是3∶2,两队共同施工6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队共同施工6天完成任务后,学校付给他们4000元报酬,若按各自完成的工程量分配这笔钱,问甲、乙两队各应得到多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com