
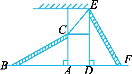
【题目】如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则直线BC与EF的位置关系是____﹒
 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
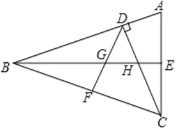
【题目】如图,CD 和 BE 是△ABC 的两条高,∠BCD=45°,BF=FC,BE与 DF、DC分别交于点 G、H,∠ACD=∠CBE.
(1)证明:AB=BC;
(2)判断 BH 与 AE 之间的数量关系,并证明你的结论;
(3)结合已知条件,观察图形,你还能发现什么结论?请写出两个(不与前面结论相同).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
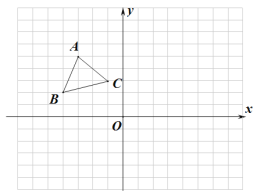
【题目】如图在平面直角坐标系中,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
(1)请你在所给的平面直角坐标系中,画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)将(1)中得到的![]() 向下移动4个单位得到
向下移动4个单位得到![]() ,画出
,画出![]() ;
;
(3)在![]() 中有一点
中有一点![]() ,直接写出经过以上两次图形变换后
,直接写出经过以上两次图形变换后![]() 中对应点
中对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D两点将线段AB分为三部分,AC:CD:DB=2:3:4,且AC=4.M是线段AB的中点,N是线段DB的中点.
(1)求线段DB、AB的长.
(2)求线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α.
(1)如图1,当α=60°时,求证:△DCE是等边三角形;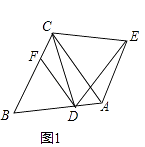
(2)如图2,当α=45°时,求证:① ![]() =
= ![]() ;②CE⊥DE.
;②CE⊥DE.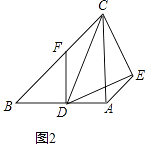
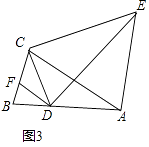
(3)如图3,当α为任意锐角时,请直接写出线段CE与DE的数量关系是: ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣(k+1)x+k与x轴相交于A、B两点(点B位于点A的左侧),与y轴相交于点C.
(1)如图1,若k=2,直接写出AB的长:AB= . 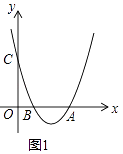
(2)若AB=2,则k的值为 .
(3)如图2,若k=﹣3,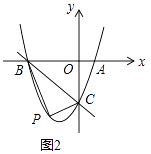
①求直线BC的解析式;
(4)如图3,若k<0,且△ABC是等腰三角形,求k的值.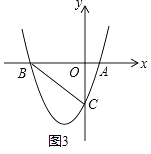
查看答案和解析>>
科目:初中数学 来源: 题型:
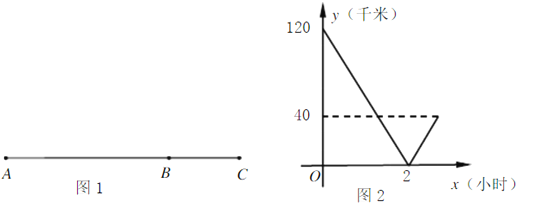
【题目】如图1,元旦期间,小明乘汽车从![]() 地出发,经过
地出发,经过![]() 地到目的地
地到目的地![]() 地(三地在同一条直线上),假设汽车从
地(三地在同一条直线上),假设汽车从![]() 到
到![]() 的过程都是匀速直线行驶.图2表示小明离
的过程都是匀速直线行驶.图2表示小明离![]() 地的路程
地的路程![]() (km)与汽车从
(km)与汽车从![]() 出发后行驶时间
出发后行驶时间![]() (h)之何的函数关系图象.
(h)之何的函数关系图象.
(1) ![]() 两地间的路程为 km;
两地间的路程为 km;
(2)求小明离![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)当行驶时间![]() 在什么范围时,汽车离
在什么范围时,汽车离![]() 地的路程不超过40 km?
地的路程不超过40 km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com