
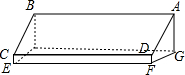
 “蔬菜大王“老杨建造了一个育苗温室(如图).温室南墙高DF=0.3m,北墙高AG=1.6m,温室下底面是长方形,长EF=8m,宽FG=3m,求温室玻璃盖ABCD的面积(结果保留一位小数).
“蔬菜大王“老杨建造了一个育苗温室(如图).温室南墙高DF=0.3m,北墙高AG=1.6m,温室下底面是长方形,长EF=8m,宽FG=3m,求温室玻璃盖ABCD的面积(结果保留一位小数). 科目:初中数学 来源: 题型:选择题
| A. | 抛掷一枚硬币,落地时正面朝上 | B. | 任意打开数学教科书,正好是58页 | ||
| C. | 两个负数相乘,结果为正数 | D. | 两个无理数相加,结果仍是无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
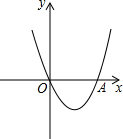 如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.
如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 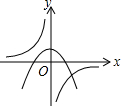 | B. | 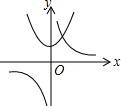 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.
如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
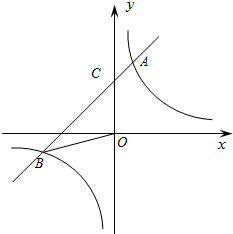 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com