
分析 (1)把a=1,b=-4,c=3代入△=b2-4ac,然后计算△,最后根据计算结果判断方程根的情况;
(2)①首先把常数项移到方程右边,再将方程两边同时加上一次项系数一半的平方,把左边配成一个完全平方式,右边化为一个常数,继而求得答案;
②将方程的左边分解为两个一次因式的乘积,令每个因式分别为零,得到两个一元一次方程,进而求解即可;
(3)根据解一元二次方程的基本思想是降次即可作答;
(4)利用因式分解法求解即可求得答案.
解答 解:(1)∵a=1,b=-4,c=3,
∴△=b2-4ac=(-4)2-4×1×3=4>0,
∴方程有两个不相等的实数根;
(2)①∵x2-4x+3=0,
∴x2-4x=-3,
∴x2-4x+4=-3+4,
∴(x-2)2=1,
∴x-2=±1,
解得:x1=3,x2=1;
②∵x2-4x+3=0,
∴(x-3)(x-1)=0,
∴x-3=0或x-1=0,
解得:x1=3,x2=1;
(3)这些方法都是将解一元二次方程转化为解一元一次方程;
(4)∵x3-x=0,
∴x(x+1)(x-1)=0,
∴x=0或x+1=0或x-1=0,
解得:x1=0,x2=-1,x3=1.
故答案为一元二次方程,一元一次方程.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了用配方法和因式分解法解一元二次方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
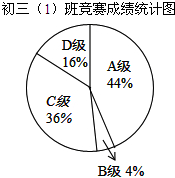 初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )
初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )| A. | B级人数比A级人数少21 | B. | 50人得分的众数是22 | ||
| C. | 50人得分的平均数是80 | D. | 50人得分的中位数是80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<n | B. | m>n | C. | m=n | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com