
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
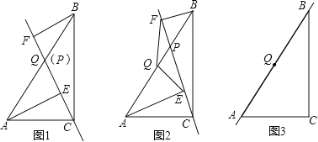
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
【答案】解:(1)AE∥BF,QE=QF。
(2)QE=QF,证明如下:
如图,延长FQ交AE于D,
![]()
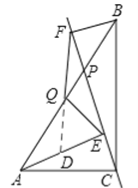
∵AE∥BF,∴∠QAD=∠FBQ。
在△FBQ和△DAQ中,∵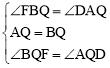 ,
,
∴△FBQ≌△DAQ(ASA)。∴QF=QD。
∵AE⊥CP,∴EQ是直角三角形DEF斜边上的中线。
∴QE=QF=QD,即QE=QF。
(3)(2)中的结论仍然成立。证明如下:
如图,延长EQ、FB交于D,
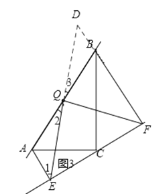
∵AE∥BF,∴∠1=∠D。
在△AQE和△BQD中,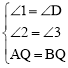 ,
,
∴△AQE≌△BQD(AAS),∴QE=QD。
∵BF⊥CP,∴FQ是斜边DE上的中线。∴QE=QF。
【解析】(1)证△BFQ≌△AEQ即可。理由是:
如图,∵Q为AB中点,∴AQ=BQ。
∵BF⊥CP,AE⊥CP,∴BF∥AE,∠BFQ=∠AEQ。
在△BFQ和△AEQ中,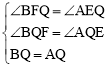 ,∴△BFQ≌△AEQ(AAS)。∴QE=QF。
,∴△BFQ≌△AEQ(AAS)。∴QE=QF。
(2)证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可。
(3)证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可。


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一堆有红、白两种颜色的球若干个,已知白球的个数比红球少,但白球的2倍比红球多.若把每一个白球都记作“2”,每一个红球都记作“3”,则总数为“60”,那么这两种球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )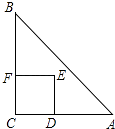
A.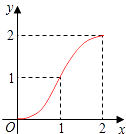
B.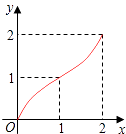
C.
D.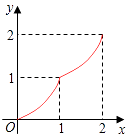
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)填空:
①A、B两点间的距离AB= ,线段AB的中点表示的数为 ;
②用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)求当t为何值时,PQ=![]() AB;
AB;
(3)当点P运动到点B的右侧时,PA的中点为M,N为PB的三等分点且靠近于P点,求PM﹣![]() BN的值.
BN的值.
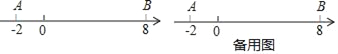
查看答案和解析>>
科目:初中数学 来源: 题型:
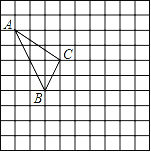
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 .
(4)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ![]() ∠CAB.
∠CAB. 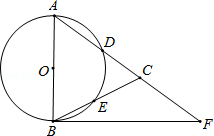
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州旅游文化节开幕前,某凤凰茶叶公司预测今年凤凰茶叶能够畅销,就用32000元购进了一批凤凰茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批凤凰茶叶,所购数量是第一批购进数量的2倍,但每千克凤凰茶叶进价多了10元.
(1)该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强市民的节能意识,我市试行阶梯电价.从2013年开始,按照每户每年的分三个档次计费,具体规定见下图.小明统计了自己2013年前5个月的实际用电量为1300度,请帮助小明分析下面问题.

(1)若小明家计划2013年全年的用电量不超过2520度,则6至12月份小明家平均每月用电量最多为多少度?(保留整数)
(2)若小明家2013年6月至12月份平均每月用电量等于前5个月的平均每月用电量,则小明家2013年应交总电费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com