
”¾ĢāÄæ”æĪŖĮĖ½āijŠ£Ń§ÉśµÄÉķøßĒéæö£¬Ė껜³éČ”øĆŠ£ÄŠÉś”¢Å®Éś½ųŠŠ³éŃłµ÷²é£®ŅŃÖŖ³éČ”µÄŃł±¾ÖŠ£¬ÄŠÉś”¢Å®ÉśµÄČĖŹżĻąĶ¬£¬ĄūÓĆĖłµĆŹż¾Ż»ęÖĘČēĻĀĶ³¼ĘĶ¼±ķ£ŗ
ÉķøßĒéæö·Ö×é±ķ£Øµ„Ī»£ŗcm£©
×鱚 | Éķøß |
A | x£¼155 |
B | 155”Üx£¼160 |
C | 160”Üx£¼165 |
D | 165”Üx£¼170 |
E | x”Ż170 |
øł¾ŻĶ¼±ķĢį¹©µÄŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ńł±¾ÖŠ£¬ÄŠÉśµÄÉķøßÖŚŹżŌŚ”” ””×飬֊Ī»ŹżŌŚ”” ””×飻
£Ø2£©Ńł±¾ÖŠ£¬Å®ÉśÉķøßŌŚE×éµÄČĖŹżÓŠ”” ””ČĖ£»
£Ø3£©ŅŃÖŖøĆŠ£¹²ÓŠÄŠÉś400ČĖ£¬Å®Éś380ČĖ£¬Ēė¹Ą¼ĘÉķøßŌŚ160”Üx£¼170Ö®¼äµÄѧɜŌ¼ÓŠ¶ąÉŁČĖ£æ

”¾“š°ø”æ£Ø1£©B”¢C£»£Ø2£©2£»£Ø3£©332ČĖ
”¾½āĪö”æ
£Ø1£©øł¾ŻÖŚŹżµÄ¶ØŅ壬ŅŌ¼°ÖŠĪ»ŹżµÄ¶ØŅå½ā“š¼“æÉ£»
£Ø2£©ĻČĒó³öÅ®ÉśÉķøßŌŚE×éĖłÕ¼µÄ°Ł·Ö±Č£¬ŌŁĒó³ö×ÜČĖŹżČ»ŗó¼ĘĖć¼“æÉµĆ½ā£»
£Ø3£©·Ö±šÓĆÄŠ”¢Å®ÉśµÄČĖŹż³ĖŅŌC”¢DĮ½×éµÄʵĀŹµÄŗĶ£¬¼ĘĖć¼“æÉµĆ½ā£®
½ā£ŗ”ßB×éČĖŹż×ī¶ą£¬
”ąÖŚŹżŌŚB×飬
ÄŠÉś×ÜČĖŹżĪŖ4+12+10+8+6£½40£¬
°“ÕÕ“ÓµĶµ½øßµÄĖ³Šņ£¬µŚ20”¢21Į½ČĖ¶¼ŌŚC×飬
”ąÖŠĪ»ŹżŌŚC×飬
¹Ź“š°øĪŖ£ŗB”¢C£»
£Ø2£©Å®ÉśÉķøßŌŚE×éµÄʵĀŹĪŖ£ŗ1©17.5%©37.5%©25%©15%£½5%£¬
”ß³éČ”µÄŃł±¾ÖŠ£¬ÄŠÉś”¢Å®ÉśµÄČĖŹżĻąĶ¬£¬
”ąŃł±¾ÖŠ£¬Å®ÉśÉķøßŌŚE×éµÄČĖŹżÓŠ40”Į5%£½2ČĖ£¬
¹Ź“š°øĪŖ£ŗ2£»
£Ø3£©400”Į![]() +380”Į£Ø25%+15%£©£½180+152£½332£ØČĖ£©£®
+380”Į£Ø25%+15%£©£½180+152£½332£ØČĖ£©£®
“š£ŗ¹Ą¼ĘøĆŠ£ÉķøßŌŚ160”Üx£¼170Ö®¼äµÄѧɜŌ¼ÓŠ332ČĖ£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµČŃü”÷ABCÖŠ£¬¶„½Ē”ĻA=36”ć£¬BDĪŖ”ĻABCµÄĘ½·ÖĻߣ¬ĒóÖ¤£ŗµćDŹĒACµÄ»Ę½š·Öøīµć£® 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
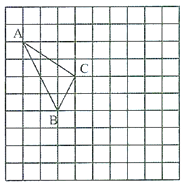
”¾ĢāÄæ”æŌŚČēĶ¼ĖłŹ¾µÄÕż·½ŠĪĶųøńÖŠ£¬ĆæøöŠ”Õż·½ŠĪµÄ±ß³¤ĪŖ1£¬øńµćČż½ĒŠĪ”÷ABCµÄ¶„µćA”¢CµÄ×ų±ź·Ö±šĪŖ(£4£¬5)£¬(£1£¬3).
£Ø1£©ĒėŌŚČēĶ¼ĖłŹ¾µÄĶųøńĘ½ĆęÄŚ×÷³öĘ½ĆęÖ±½Ē×ų±źĻµ£»
£Ø2£©Ēė°Ń”÷ABCĻČĻņÓŅŅʶÆ5øöµ„Ī»£¬ŌŁĻņĻĀĘ½ŅĘ3øöµ„Ī»µĆµ½”÷![]() £¬ŌŚĶ¼ÖŠ»³ö”÷
£¬ŌŚĶ¼ÖŠ»³ö”÷![]() £»
£»
£Ø3£©Ēó”÷ABCµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
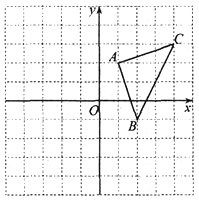
”¾ĢāÄæ”æČēĶ¼£¬Ę½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷ABCµÄ¶„µć×ų±źĪŖ£ŗA(1£¬2)£¬B(2£¬ Ņ»1)£¬ C (4£¬ 3)£®
(1)½«”÷ABCĻņ×óĘ½ŅĘ2øöµ„Ī»³¤¶Č£¬ŌŁĻņÉĻĘ½ŅĘ1øöµ„Ī»³¤¶Č£¬µĆ”÷A£§B£§C£§£®»³ö”÷A£§B£§C£§£¬²¢Š“³ö”÷A£§B£§C£§µÄ¶„µć×ų±ź£»
(2)Ēó”÷ABCµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹż¾Żx1£¬x2£¬”£¬xnµÄ·½²īĪŖA£¬ŌņŹż¾Ż3x1+1£¬3x2+1£¬”3xn+1µÄ·½²īĪŖ£Ø””””£©
A. 3A B. 3A+1 C. 9A D. 9A+1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬MŹĒĘ½ŠŠĖıߊĪABCDµÄAB±ßÖŠµć£¬CM½»BDÓŚµćE£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ÓėĘ½ŠŠĖıߊĪABCDµÄĆ껿µÄ±ČŹĒ£Ø £©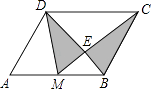
A.1£ŗ3
B.1£ŗ4
C.1£ŗ6
D.5£ŗ12
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒŅ»ÕÅĘ½ŠŠĖıߊĪÖ½Ę¬ABCD£¬ŅŖĒóĄūÓĆĖłŃ§ÖŖŹ¶½«Ėü±ä³ÉŅ»øöĮāŠĪ£¬¼×”¢ŅŅĮ½Ī»Ķ¬Ń§µÄ×÷·Ø·Ö±šČēĻĀ£ŗ

¶ŌÓŚ¼×”¢ŅŅĮ½ČĖµÄ×÷·Ø£¬æÉÅŠ¶Ļ(””””)
A. ¼×ÕżČ·£¬ŅŅ“ķĪó B. ¼×“ķĪó£¬ŅŅÕżČ·
C. ¼×”¢ŅŅ¾łÕżČ· D. ¼×”¢ŅŅ¾ł“ķĪó
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŹĢā£ŗĢ½¾æŗÆŹży£½|x|©2µÄĶ¼ĻóÓėŠŌÖŹ£®
Š”»Ŗøł¾ŻŃ§Ļ°ŗÆŹżµÄ¾Ń飬¶ŌŗÆŹży£½|x|©2µÄĶ¼ĻóÓėŠŌÖŹ½ųŠŠĮĖĢ½¾æ£®
ĻĀĆęŹĒŠ”»ŖµÄĢ½¾æ¹ż³Ģ£¬Ēė²¹³äĶźÕū£ŗ
£Ø1£©ŌŚŗÆŹży£½|x|©2ÖŠ£¬×Ō±äĮæxæÉŅŌŹĒČĪŅāŹµŹż£»
£Ø2£©Čē±ķŹĒyÓėxµÄ¼ø×é¶ŌÓ¦Öµ
x | ” | ©3 | ©2 | ©1 | 0 | 1 | 2 | 3 | ” |
y | ” | 1 | 0 | ©1 | ©2 | ©1 | 0 | m | ” |
¢ŁmµČÓŚ¶ąÉŁ£»
¢ŚČōA£Øn£¬2018£©£¬B£Ø2020£¬2018£©ĪŖøĆŗÆŹżĶ¼ĻóÉĻ²»Ķ¬µÄĮ½µć£¬ŌņnµČÓŚ¶ąÉŁ£»
£Ø3£©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ćč³öŅŌÉĻ±ķÖŠø÷¶Ō¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£¬²¢øł¾ŻĆč³öµÄµć»³öøĆŗÆŹżµÄĶ¼Ļó£»øł¾ŻŗÆŹżĶ¼ĻóæÉµĆ£ŗøĆŗÆŹżµÄ×īŠ”ÖµĪŖ¶ąÉŁ£»øĆŗÆŹżĶ¼ĻóÓėxÖįĪ§³ÉµÄ¼øŗĪĶ¼ŠĪµÄĆ껿µČÓŚ¶ąÉŁ£»
£Ø4£©ŅŃÖŖÖ±Ļßy1£½![]() x©
x©![]() ÓėŗÆŹży£½|x|©2µÄĶ¼Ļó½»ÓŚC£¬DĮ½µć£¬µ±y1”ŻyŹ±£¬ŹŌČ·¶ØxµÄȔֵ·¶Ī§£®
ÓėŗÆŹży£½|x|©2µÄĶ¼Ļó½»ÓŚC£¬DĮ½µć£¬µ±y1”ŻyŹ±£¬ŹŌČ·¶ØxµÄȔֵ·¶Ī§£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĢ½Ė÷£ŗŠ”Ć÷ŌŚŃŠ¾æŹżŃ§ĪŹĢā£ŗŅŃÖŖAB”ĪCD£¬ABŗĶCD¶¼²»¾¹żµćP£¬Ģ½Ė÷”ĻPÓė”ĻCµÄŹżĮæ¹ŲĻµ£®

·¢ĻÖ£ŗŌŚČēĶ¼ÖŠ£¬£ŗ”ĻAPC=”ĻA+”ĻC£»ČēĶ¼
Š”Ć÷ŹĒÕāŃłÖ¤Ć÷µÄ£ŗ¹żµćP×÷PQ”ĪAB
”ą”ĻAPQ=”ĻA(_ __)
”ßPQ”ĪAB,AB”ĪCD.
”ąPQ”ĪCD(__ _)
”ą”ĻCPQ=”ĻC
”ą”ĻAPQ+”ĻCPQ=”ĻA+”ĻC
¼“”ĻAPC=”ĻA+”ĻC
(1)ĪŖŠ”Ć÷µÄÖ¤Ć÷ĢīÉĻĶĘĄķµÄŅĄ¾Ż£»
(2)Ó¦ÓĆ£ŗ¢ŁŌŚČēĶ¼ÖŠ£¬”ĻPÓė”ĻA”¢”ĻCµÄŹżĮæ¹ŲĻµĪŖ__ _£»
¢ŚŌŚČēĶ¼ÖŠ,Čō”ĻA=30![]() £¬”ĻC=70
£¬”ĻC=70![]() £¬Ōņ”ĻPµÄ¶ČŹżĪŖ__ _£»
£¬Ōņ”ĻPµÄ¶ČŹżĪŖ__ _£»
(3)ĶŲÕ¹£ŗŌŚČēĶ¼ÖŠ£¬Ģ½¾æ”ĻPÓė”ĻA,”ĻCµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com