
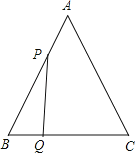
【题目】已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:
(1)经过![]() 秒时,求△PBQ的面积;
秒时,求△PBQ的面积;
(2)当t为何值时,△PBQ是直角三角形?
(3)是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.
【答案】(1)![]() ;(2)t=1秒或t=2秒时,△PBQ是直角三角形.(3)无论t取何值,四边形APQC的面积都不可能是△ABC面积的
;(2)t=1秒或t=2秒时,△PBQ是直角三角形.(3)无论t取何值,四边形APQC的面积都不可能是△ABC面积的![]() .
.
【解析】试题分析:(1)根据路程=速度×时间,求出BQ,AP的值,再求出BP的值,然后利用三角形的面积公式进行解答即可;
(2)①∠BPQ=90°;②∠BQP=90°.然后在直角三角形BQP中根据BP,BQ的表达式和∠B的度数进行求解即可.
(3)本题可先用△ABC的面积-△PBQ的面积表示出四边形APQC的面积,即可得出y,t的函数关系式,然后另y等于三角形ABC面积的三分之二,可得出一个关于t的方程,如果方程无解则说明不存在这样的t值,如果方程有解,那么求出的t值即可
试题解析:(1)经过![]() 秒时,AP=
秒时,AP=![]() cm,BQ=
cm,BQ=![]() cm,
cm,
∵△ABC是边长为3cm的等边三角形,
∴AB=BC=3cm,∠B=60°,
∴BP=3-![]() =
=![]() cm,
cm,
∴△PBQ的面积=![]() BPBQsin∠B=
BPBQsin∠B=![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() ;
;
(2)设经过t秒△PBQ是直角三角形,
则AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3-t)cm,
△PBQ中,BP=(3-t)cm,BQ=tcm,若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ=![]() BP,
BP,
即t=![]() (3-t),t=1(秒),
(3-t),t=1(秒),
当∠BPQ=90°时,BP=![]() BQ,
BQ,
3-t=![]() t,t=2(秒),
t,t=2(秒),
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
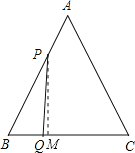
(3)过P作PM⊥BC于M,
△BPM中,sin∠B=![]() ,
,
∴PM=PBsin∠B=![]() (3-t),
(3-t),
∴S△PBQ=![]() BQPM=
BQPM=![]() t
t![]() (3-t),
(3-t),
∴y=S△ABC-S△PBQ=![]() ×32×
×32×![]() -
-![]() ×t×
×t×![]() (3-t)
(3-t)
=![]() t2-
t2-![]() t+
t+![]() ,
,
∴y与t的关系式为y=![]() t2-
t2-![]() t+
t+![]() ,
,
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的![]() ,
,
则S四边形APQC=![]() S△ABC,
S△ABC,
∴![]() t2-
t2-![]() t+
t+![]() =
=![]() ×
×![]() ×32×
×32×![]() ,
,
∴t2-3t+3=0,
∵(-3)2-4×1×3<0,
∴方程无解,
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的![]() .
.


科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 对角线互相垂直的四边形是菱形
B. 一组对边相等,另一组对边平行的四边形是平行四边形
C. 对角线相等的四边形是矩形
D. 对角线互相垂直平分且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地.货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示.
(1)甲乙两地相距多远?小轿车中途停留了多长时间?
(2)①写出y1与x的函数关系式;
②当x≥5时,求y2与x的函数解析式;
(3)货车出发多长时间与小轿车首次相遇?相遇时与甲地的距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)=![]() .如:12=1×12=2×6=3×4,则F(12)=
.如:12=1×12=2×6=3×4,则F(12)=![]() .则在以下结论:①F(5)=5;②F(24)=
.则在以下结论:①F(5)=5;②F(24)=![]() ;③若a是一个完全平方数,则F(a)=1;④若a是一个完全立方数,即a=x3(x是正整数),则F(a)=x.则正确的结论有_____(填序号)
;③若a是一个完全平方数,则F(a)=1;④若a是一个完全立方数,即a=x3(x是正整数),则F(a)=x.则正确的结论有_____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,不正确的是( )
A. 菱形的四条边相等 B. 平行四边形的邻边相等
C. 对角线相等的平行四边形是矩形 D. 正方形的对角线相等且互相垂直平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五名女生的体重(单位:kg)分别为:37、40、38、42、42,这组数据的众数和中位数分别是( )
A. 2、40 B. 42、38 C. 40、42 D. 42、40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com