
【题目】如图,△ABC和△CDE都是等边三角形,B,C,D三点在一条直线上,AD与BE交于点P,AC,BE交于点M,AD,CE交于点N,连接MN,则下列五个结论:①AD=BE;②∠BMC=∠ANE;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中一定正确的是__________.(填出所有正确结论的序号)

【答案】①③④⑤
【解析】
根据先证明△BCE≌△ACD,得出AD=BE,根据已知给出的条件即可得出答案.
∵△ABC和△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠ECD=60°,∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,∴△BCE≌△ACD(SAS),∴AD=BE,故①正确;
∵△BCE≌△ACD,∴∠CBE=∠CAD.
∵∠ACB=∠ACE=60°,∴∠BMC=∠ANC,故②错误;
∵△BCE≌△ACD,∴∠CBE=∠CAD.
∵∠BMC=∠AMP,∴∠APM=∠ACB=60°,故③正确;
在△ACN和△BCM中,∵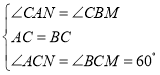 ,∴△ACN≌△BCM,∴AN=BM,故④正确;
,∴△ACN≌△BCM,∴AN=BM,故④正确;
△ACN≌△BCM,∴CM=CN,∴△CMN为等腰三角形.
∵∠MCN=60°,∴△CMN是等边三角形,故⑤正确.
故答案为:①③④⑤.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.

(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
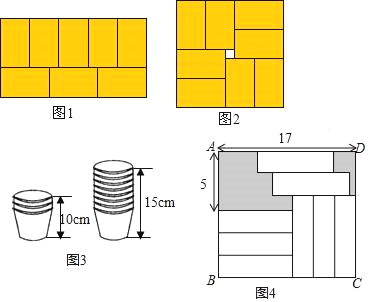
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是 cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:

(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面坐标系中,ΔABC是等腰直角三角形,∠ABC=90°,AB=BC,点A坐标为(-8,-3),点B坐标为(0,-5),AC交x轴于点D.

(1)求点C和D的坐标;
(2)点M在x轴上,当ΔAMB的周长最小时,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com