Question

【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE并延长,交BC的延长线于点F.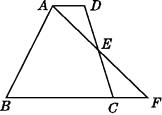

（1）求证:CF=AD.
（2）若AD=2,AB=8,当BC的长为多少时,点B在线段AF的垂直平分线上?为什么?

Answer 1

【答案】
（1）证明:证明:∵AD∥BC,
∴∠ECF=∠ADE.
∵E为CD的中点,
∴CE=DE ，
在△FEC与△AED中
,
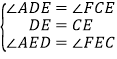
∴△FEC≌△AED(ASA).
∴CF=AD.
（2）解:当BC=6时,点B在线段AF的垂直平分线上.理由如下:
∵BC=6,AD=2,AB=8,
∴AB=BC+AD.
又∵CF=AD,BC+CF=BF,
∴AB=BF.
∴点B在AF的垂直平分线上 。
【解析】（1）根据二直线平行内错角相等得出∠ECF=∠ADE，根据中点的定义得出CE=DE ，然后根据ASA判断出△FEC≌△AED ，根据全等三角形对应边相等得出CF=AD；
（2）当BC=6时,点B在线段AF的垂直平分线上.当BC=6,AD=2,AB=8,时 ，根据线段的长度得出AB=BC+AD，根据线段的和差及等量代换得出AB=BF，然后根据到线段两端点距离相等得点在线段的垂直平分线上得出结论。