
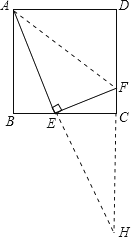
【题目】如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.
(1)求证:△ABE∽△ECF;
(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你的结论.
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF;
(2)
证明:E是中点时,∠BAE=∠EAF,
理由如下:
连接AF,延长AE于DC的延长线相交于点H,
∵E为BC中点,
∴BE=CE,
∵AB∥DH,
∴∠B=∠ECH,
∵∠AEB=∠CEH,
∴△ABE≌△HCE,
∴AE=EH,
∵EF⊥AH,
∴△AFH是等腰三角形,
∴∠EAF=∠H,
∵AB∥DH,
∴∠H=∠BAE,
∴∠BAE=∠EAF,
∴当点E在BC中点位置时,∠BAE=∠EAF.
【解析】(1)有正方形的性质和已知条件证明∠BAE=∠FEC即可证明:△ABE∽△ECF;(2)连接AF,延长AE于DC的延长线相交于点H,当点E在BC中点位置时,通过证明三角形全等和等腰三角形的性质以及平行线的性质即可证明∠BAE=∠EAF.
【考点精析】利用正方形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(﹣1,0),O是坐标原点,且|OC|=3|OA|
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC, 连接 CE、OE,连接AE交OD于点F.(1)求证:OE=CD (2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长度,数![]() 在数轴上表示的点在原点右侧,距离原点4个单位长度,c和d互为倒数,m和n互为相反数,
在数轴上表示的点在原点右侧,距离原点4个单位长度,c和d互为倒数,m和n互为相反数,![]() 是最大的负整数,求
是最大的负整数,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)体育课上,某中学对七年级男生进行了引体向上测试,以能做7个为标准多于标准的次
数记为正数,不足的次数记为负数,其中8名男生的成绩为+2,-1,+3,0,-2,-3,+1,0.
(1)这8名男生中达到标准的占百分之几?
(2)他们共做了多少次引体向上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济的高速发展,有着“经济晴雨表”之称的股市也得到迅速的发展,下表是今年上证指数某一周星期一至星期五的变化情况. (注:上周五收盘时上证指数为2616点,每一天收盘时指数与前一天相比,涨记为“+”,跌记为“-”)
星 期 | 一 | 二 | 三 | 四 | 五 |
指数的变化(与前一天比较) |
|
|
|
|
|
⑴ 请求出这一周星期五收盘时的上证指数是多少点?
⑵ 说出这一周每一天收盘时上证指数哪一天最高?哪一天最低?分别是多少点?
查看答案和解析>>
科目:初中数学 来源: 题型:
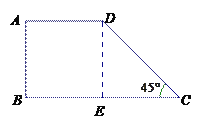
【题目】为了增强学生体质,学校鼓励学生多参加体育锻炼,小华同学马上行动,每天围绕小区进行晨跑锻炼.该小区外围道路近似为如图所示四边形ABCD,已知四边形ABED为正方形,∠DCE=45°,AB=100米.小华某天绕该道路晨跑5圈,求小华该天晨跑的路程是多少?(结果保留整数,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°.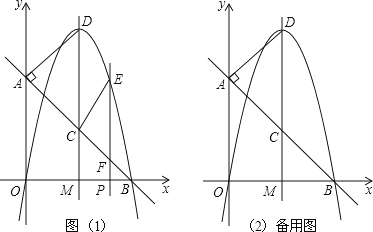
(1)直接写出直线AB的解析式;
(2)求点D的坐标;
(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O、D、B三点的抛物线于点E,连接CE.是否存在点P,使△BPF与△FCE相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com