
【题目】已知抛物线y=ax2﹣2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(﹣1,0),O是坐标原点,且|OC|=3|OA|
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
【答案】
(1)
答案
解:∵A(﹣1,0),|OC|=3|OA|
∴C(0,﹣3)
∵抛物线经过A(﹣1,0),
C(0,﹣3)
∴ ![]()
∴ ![]()
∴y=x2﹣2x﹣3
;
答案
解:∵A(﹣1,0),|OC|=3|OA|
∴C(0,﹣3)
∵抛物线经过A(﹣1,0),
C(0,﹣3)
∴ ![]()
∴ ![]()
∴y=x2﹣2x﹣3
;答案;解:∵A(﹣1,0),|OC|=3|OA|
∴C(0,﹣3)
∵抛物线经过A(﹣1,0),
C(0,﹣3)
∴ ![]()
∴ ![]()
∴y=x2﹣2x﹣3
(2)
解:)由(1)的抛物线知:点B(3,0);
设直线BC的解析式为:y=kx﹣3,代入B点坐标,得:
3k﹣3=0,解得 k=1
∴直线BC的函数表达式为y=x﹣3
(3)
解:当正方形ODEF的顶点D运动到直线BC上时,设D点的坐标为(m,﹣2),
根据题意得:﹣2=m﹣3,∴m=1.
①当0<t≤1时,正方形和△OBC的重合部分是矩形;
∵OO1=t,OD=2
∴S1=2t;
当1<t≤2时,正方形和△OBC的重合部分是五边形,如右图;
∵OB=OC=3,∴△OBC、△D1GH都是等腰直角三角形,∴D1G=D1H=t﹣1;
S2=S矩形DD1O1O﹣S△D1HG=2t﹣ ![]() ×(t﹣1)2=﹣
×(t﹣1)2=﹣ ![]() t2+3t﹣
t2+3t﹣ ![]() .
.
②由①知:
当0<t≤1时,S=2t的最大值为2;
当1<t≤2时,S=﹣ ![]() t2+3t﹣
t2+3t﹣ ![]() =﹣
=﹣ ![]() (t﹣3)2+4,由于未知数的取值范围在对称轴左侧,且抛物线的开口向下;
(t﹣3)2+4,由于未知数的取值范围在对称轴左侧,且抛物线的开口向下;
∴当t=2时,函数有最大值,且值为 S=﹣ ![]() +4=
+4= ![]() >2.
>2.
综上,当t=2秒时,S有最大值,最大值为 ![]()
(4)
解:

由(2)知:点P(1,﹣2).假设存在符合条件的点M;
①当AM ![]() PN时,点N、P的纵坐标相同,即点N的纵坐标为﹣2,代入抛物线的解析式中有:
PN时,点N、P的纵坐标相同,即点N的纵坐标为﹣2,代入抛物线的解析式中有:
x2﹣2x﹣3=﹣2,解得 x=1± ![]() ;
;
∴AM=NP= ![]() ,
,
∴M1(﹣ ![]() ﹣1,0)、M2(
﹣1,0)、M2( ![]() ﹣1,0).
﹣1,0).
②当AN ![]() PM时,平行四边形的对角线PN、AM互相平分;
PM时,平行四边形的对角线PN、AM互相平分;
设M(m,0),则 N(m﹣2,2),代入抛物线的解析式中,有:
(m﹣2)2﹣2(m﹣2)﹣3=2,解得 m=3± ![]() ;
;
∴M3(3﹣ ![]() ,0)、M4(3+
,0)、M4(3+ ![]() ,0).
,0).
综上,存在符合条件的M点,且坐标为:
M1(﹣ ![]() ﹣1,0)、M2(
﹣1,0)、M2( ![]() ﹣1,0)、M3(3﹣
﹣1,0)、M3(3﹣ ![]() ,0)、M4(3+
,0)、M4(3+ ![]() ,0).
,0).
【解析】(1)首先由OC、OA的数量关系确定点C的坐标,即可利用待定系数法求出抛物线的解析式.(2)由(1)的抛物线解析式可得点B的坐标,而点C的坐标已经求得,由待定系数法求解即可.(3)①首先要明确正方形ODEF和△OBC重合部分的形状:当点D在△OBC内部时,两者的重合部分是矩形;当点D在△OBC外部时,两者的重合部分是五边形,其面积可由正方形的面积减去△DGH的面积(G、H分别为ED、OD和线段BC的交点).在判断t的取值范围时,要注意一个“关键点”:点D位于线段BC上时.②根据①的函数性质即可得到答案,要注意未知数的取值范围.(4)若存在以A、M、N、P为顶点的平行四边形,那么应分:AM ![]() PN或AN
PN或AN ![]() PM两种情况,由于AM在x轴上,结合平行四边形的特点可知:无论哪种情况,点N到x轴的距离都等于点P到x轴的距离,根据这个特点可确定点M、N的坐标.
PM两种情况,由于AM在x轴上,结合平行四边形的特点可知:无论哪种情况,点N到x轴的距离都等于点P到x轴的距离,根据这个特点可确定点M、N的坐标.
【考点精析】关于本题考查的二次函数图象的平移,需要了解平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】根据要求回答问题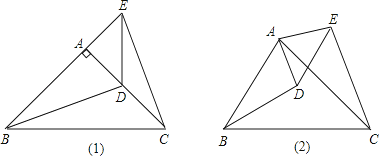
(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由.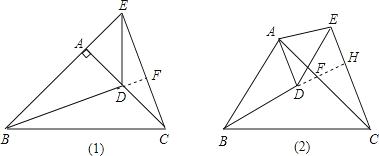
(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE在(1)中的位置关系仍然成立?不必说明理由.
甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;
乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;
丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=![]() ,OC=
,OC=![]() ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,运动到3秒钟时,两点相距15个单位长度.已知动点A、B的运动速度比之是3:2(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)A、B两点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
(3)若A、B两点分别从(2)中标出的位置再次同时开始在数轴上运动,运动的速度不变,运动的方向不限,问:经过几秒钟,A、B两点之间相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上![]() ,
,![]() 两点对应的数分别为
两点对应的数分别为![]() ,
,![]() ,且满足
,且满足![]() ;
;
![]() 求
求![]() ,
,![]() 的值;
的值;
![]() 若点
若点![]() 以每秒
以每秒![]() 个单位,点
个单位,点![]() 以每秒
以每秒![]() 个单位的速度同时出发向右运动,多长时间后
个单位的速度同时出发向右运动,多长时间后![]() ,
,![]() 两点相距
两点相距![]() 个单位长度?
个单位长度?
![]() 已知
已知![]() 从
从![]() 向右出发,速度为每秒一个单位长度,同时
向右出发,速度为每秒一个单位长度,同时![]() 从
从![]() 向右出发,速度为每秒
向右出发,速度为每秒![]() 个单位长度,设
个单位长度,设![]() 的中点为
的中点为![]() ,
,![]() 的值是否变化?若不变求其值;否则说明理由.
的值是否变化?若不变求其值;否则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△ABC关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.
(1)求证:△ABE∽△ECF;
(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com