
����Ŀ������A��ԭ����������Ḻ�����˶���ͬʱ������BҲ��ԭ������������������˶����˶���3����ʱ���������15����λ���ȣ���֪����A��B���˶��ٶȱ�֮��3��2���ٶȵ�λ��1����λ����/�룩��
��1�������������˶����ٶȣ�
��2��A��B�����˶���3��ʱֹͣ�˶������������ϱ����ʱA��B�����λ�ã�
��3����A��B����ֱ�ӣ�2���б����λ���ٴ�ͬʱ��ʼ���������˶����˶����ٶȲ��䣬�˶��ķ����ޣ��ʣ����������ӣ�A��B����֮�����4����λ���ȣ�
���𰸡���1������A���˶��ٶ�Ϊ3����λ����/�룬����B���˶��ٶ�Ϊ2����λ����/��;��2���˶���3����ʱ����A��ʾ����Ϊ��9����B��ʾ����Ϊ6��
��3������![]() ��
��![]() ��11��19�룬A��B����֮�����4����λ���ȣ�
��11��19�룬A��B����֮�����4����λ���ȣ�
�������������������1�����B���ٶ�Ϊ2x����λ����/�룬���A���ٶ�Ϊ3x����λ����/�룬�����ٶȺ͡�ʱ��=����ľ��룬���ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��2����·��=�ٶȡ�ʱ�����˶�����ɵó��˶���3����ʱ��A��B����ʾ�������ٽ������������ϼ��ɣ�
��3�����˶���ʱ��Ϊt�룬��A��B������ٶȹ�ϵ�ɷ�A��B�����������������˶���A��B������������������������A��B������˶��ٶȽ��A��B����֮�����4����λ���ȣ����ɵó�����t�ĺ�����ֵ���ŵ�һԪһ�η��̣���֮���ɵó����ۣ�
�����������1�����B���ٶ�Ϊ2x����λ����/�룬���A���ٶ�Ϊ3x����λ����/�룬
��������ã�3����2x+3x��=15��
��ã�x=1��
��3x=3��2x=2��
�𣺶���A���˶��ٶ�Ϊ3����λ����/�룬����B���˶��ٶ�Ϊ2����λ����/����
��2��3��3=9��2��3=6��
���˶���3����ʱ����A��ʾ����Ϊ��9����B��ʾ����Ϊ6��
��3�����˶���ʱ��Ϊt����
��A��B�����������������˶�ʱ����|3t��2t��15|=4��
��ã�t1=11��t2=19��
��A��B�����������ʱ����|15��3t��2t|=4��
��ã�t3=![]() ��t4=
��t4=![]() ��
��
�𣺾���![]() ��
��![]() ��11��19�룬A��B����֮�����4����λ���ȣ�
��11��19�룬A��B����֮�����4����λ���ȣ�
![]()


 ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c��������ABC�����ߵij���������a2��2b2��c2��2b(a��c)��0�����жϴ����������ߵĴ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУһ�鳤Ϊ2a�������οյ������꼶�ĸ��������������зָ����꼶��1������������һ��߳�Ϊ��a��2b���������Σ���0��b��![]() ����
����
��1���ֱ�����ߣ�2�����ߣ�3�����������������
��2���ߣ�4������������������ߣ�1��������������������ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊa������������ȥһ���߳�Ϊb��С�����Σ�a��b������ͼ�ף��������µIJ���ƴ��һ�����Σ���ͼ�ң�����������ͼ������Ӱ���ֵ������ȣ�������֤�� �� 
A.��a+b��2=a2+2ab+b2
B.��a��b��2=a2��2ab+b2
C.a2��b2=��a+b����a��b��
D.��a+2b����a��b��=a2+ab��2b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1����2����BAC��20������ACF��80��.
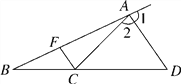
(1)���2�Ķ�����
(2)FC��ADƽ����Ϊʲô��
(3)�������Ͻ��ۣ�����ȷ����ADB���FCB�Ĵ�С��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������3��4��6��8��8��9����λ���������ֱ��ǣ�������
A.7��8B.7��8��5C.5��8D.7��5��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���A��x1,y1����B��x2,y2������x1x2+y1y2=0�����A��B��Ϊ�����㣬��A����B�������㣬BҲ����A�������㡣���磺A��1,1����B��2��-2������1��2+1����-2��=0����A��B��Ϊ�����㡣
��1����ֱ������ϵxOy�У�OΪ����ԭ�㣬�ж�����˵���Ƿ���ȷ���Ե�д����ȷ��������д��������
��ԭ���������������㡣
��x���ϵ��������y���ϵ�����㶼��Ϊ�����㡣
�۵�M��N��Ϊ�����㣬���MON=90��.
�ܵ�M��N��Ϊ�����㣬��OM=ON��
��2����P��Q��Ϊ�����㣬P������Ϊ��2��-3����Q������Ϊ��6��m������m��ֵ��
��3����M��ֱ��y=2x+1�ϵ�һ�㣬��M��N��3��-1����Ϊ�����㣬��MN�ij��ȡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�չ涨��һ��������*����a��b������������a*b=3a��2b��С�������2*5=��4�������С�ռ���2*����5��= ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com