
【题目】已知一次函数的图像经过点A(0,4) ,且与两坐标轴围成的三角形面积是8,则这个函数的解析式是( )
A. ![]() 或
或![]() B.
B. ![]() 或
或![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
【题目】填空并解答相关问题:
(1)观察下列数1,3,9,27,81…,发现从第二项开始,每一项除以前一项的结果是一个常数,这个常数是________;根据此规律,如果an (n为正整数)表示这列数的第n项,那么an =__________;
你能求出它们的和吗?
计算方法:如果要求1+3+32+33+…+320的值,
可令S=1+3+32+33+…+320①
将①式两边同乘以3,得3S=3+32+33+…+320+321②
由②式左右两边分别减去①式左右两边,
得3S-S=(3+32+33+…+320+321)-(1+3+32+33+…+320),
即2S=321-1,两边同时除以2得![]() .
.
(2)你能用类比的思想求1+6+62+63+…+6100的值吗?写出求解过程.
(3)你能用类比的思想求1+m+m2+m3+…+mn(其中mn≠0,m≠1)的值吗?写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)画出△ABC关于直线L的对称图形.

(2)如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现![]() 是_______三角形.
是_______三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,∠B=∠C,BC=8,点D从B点出发沿线段BC向C运动(D不与B、C重合),点E从点C出发沿线段CA向A运动(E不与A、C重合),它们以相同的速度同时运动,连结AD、DE.若要使△ABD≌△DCE,①请给出确定D、E两点位置的方法(如指明CD长度等),并说明理由;②此时∠ADE与∠C大小关系怎样?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,那么下列条件中不能判定四边形
,那么下列条件中不能判定四边形![]() 是菱形的为( )
是菱形的为( )
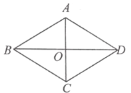
A. ∠OAB=∠OBAB. ∠OBA=∠OBCC. AD∥BCD. AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的![]() 件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人,甲加工新产品的数量要比乙多
件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人,甲加工新产品的数量要比乙多![]() .
.
(1)求甲、乙两人各需加工多少件新产品;
(2)已知乙比甲平均每天少加工![]() 件新产品,用时比甲多用
件新产品,用时比甲多用![]() 天时间.求甲平均每天加工多少件新产品.
天时间.求甲平均每天加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知: ![]() ,求
,求![]() 的值为_____;
的值为_____;
(2)当式子![]() 有最大值时,最大值是 .
有最大值时,最大值是 .
(3)材料:在学习绝对值时,我们知道了绝对值的几何含义,如|5-3|表示5、3在数轴上对应的两点之间的距离:|5+3|=|5-(-3)|,所以|5+3|表示5、-3在数轴上对应的两点之间的距离:那么![]() 的最小值是
的最小值是
(4)求![]() 的最小值以及取最小值时
的最小值以及取最小值时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
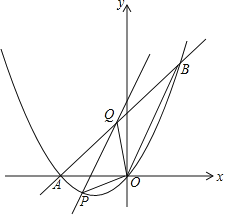
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=﹣2.
(1)求抛物线的解析式;
(2)设直线y=kx+4与抛物线两交点的横坐标分别为x1,x2(x1<x2),当![]() 时,求k的值;
时,求k的值;
(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点Q,当S△POQ:S△BOQ=1:2时,求出点P的坐标.
(坐标平面内两点M(x1,y1),N(x2,y2)之间的距离MN=![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com