
【题目】(1)画出△ABC关于直线L的对称图形.

(2)如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现![]() 是_______三角形.
是_______三角形.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读并解答问题:
数学大师的名题与方程
欧拉是18世纪瑞士著名的数学大师.他的一生都致力于数学各个领域的研究,并取得非凡的成就.在他所著的《代数学入门》一书中就曾经出现过好几道和遗产分配有关的数学问题.他构思这些问题的初衷,正是为了强化方程解题的适用和便利.
请用适当的方法解答下面问题:
父亲死后,四个儿子按下述方式分了他的财产:老大拿了财产的一半少3000英镑:老二拿了财产的![]() 少1000英镑;老三拿了恰好是财产的
少1000英镑;老三拿了恰好是财产的![]() ;老四拿了财产的
;老四拿了财产的![]() 加上600英镑.问整个财产有多少?每个儿子各分了多少?
加上600英镑.问整个财产有多少?每个儿子各分了多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.

(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数;
(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.
(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过___________秒后边OC与边ON互相垂直.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,且满足
,且满足![]() ,
,![]() 为原点.
为原点.
(1)试求![]() 和
和![]() 的值;
的值;
(2)点![]() 从
从![]() 点出发向右运动,经过3秒后点
点出发向右运动,经过3秒后点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点距离的3倍,求点
点距离的3倍,求点![]() 的运动速度?
的运动速度?
(3)点![]() 以一个单位每秒的速度从点
以一个单位每秒的速度从点![]() 向右运动,同时点
向右运动,同时点![]() 从点
从点![]() 出发以5个单位每秒的速度向左运动,点
出发以5个单位每秒的速度向左运动,点![]() 从点
从点![]() 出发,以20个单位每秒的速度向右运动.在运动过程中,
出发,以20个单位每秒的速度向右运动.在运动过程中,![]() 分别为
分别为![]() 的中点,问
的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
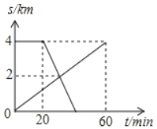
A. 8:30 B. 8:35 C. 8:40 D. 8:45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数1个1,2个![]() ,3个
,3个![]() ,…,n个
,…,n个![]() (n为正整数)顺次排成一列:1,
(n为正整数)顺次排成一列:1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,记a1=1,a2=
,…,记a1=1,a2=![]() ,a3=
,a3=![]() ,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com