
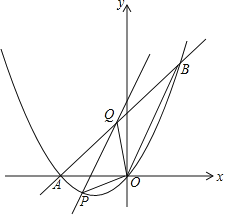
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=﹣2.
(1)求抛物线的解析式;
(2)设直线y=kx+4与抛物线两交点的横坐标分别为x1,x2(x1<x2),当![]() 时,求k的值;
时,求k的值;
(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点Q,当S△POQ:S△BOQ=1:2时,求出点P的坐标.
(坐标平面内两点M(x1,y1),N(x2,y2)之间的距离MN=![]() )
)
【答案】(1)抛物线解析式为y=![]() x2+x;(2)k=1;(3)P(﹣2
x2+x;(2)k=1;(3)P(﹣2![]() ,﹣2
,﹣2![]() +2).
+2).
【解析】(1)先利用对称轴公式得出b=4a,进而利用待定系数法即可得出结论;
(2)先利用根与系数的关系得出,x1+x2=4(k﹣1),x1x2=﹣16,转化已知条件,代入即可得出结论;
(3)先判断出OB=2PQ,进而判断出点C是OB中点,再求出AB解析式,判断出PC∥AB,即可得出PC解析式,和抛物线解析式联立解方程组即可得出结论.
(1)根据题意得,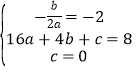 ,
,
∴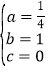 ,
,
∴抛物线解析式为y=![]() x2+x;
x2+x;
(2)∵直线y=kx+4与抛物线两交点的横坐标分别为x1,x2,
∴![]() x2+x=kx+4,
x2+x=kx+4,
∴x2﹣4(k﹣1)x﹣16=0,
根据根与系数的关系得,x1+x2=4(k﹣1),x1x2=﹣16,
∵![]() ,
,
∴2(x1﹣x2)=x1x2,
∴4(x1﹣x2)2=(x1x2)2,
∴4[(x1+x2)2﹣4x1x2]=(x1x2)2,
∴4[16(k﹣1)2+64]=162,
∴k=1;
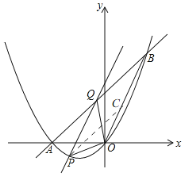
(3)如图,取OB的中点C,
∴BC=![]() OB,
OB,
∵B(4,8),
∴C(2,4),
∵PQ∥OB,
∴点O到PQ的距离等于点O到OB的距离,
∵S△POQ:S△BOQ=1:2,
∴OB=2PQ,
∴PQ=BC,∵PQ∥OB,
∴四边形BCPQ是平行四边形,
∴PC∥AB,
∵抛物线的解析式为y=![]() x2+x①,
x2+x①,
令y=0,
∴![]() x2+x=0,
x2+x=0,
∴x=0或x=﹣4,
∴A(﹣4,0),
∵B(4,8),
∴直线AB解析式为y=x+4,设直线PC的解析式为y=x+m,
∵C(2,4),
∴直线PC的解析式为y=x+2②,
联立①②解得,![]() (舍)或
(舍)或![]() ,
,
∴P(﹣2![]() ,﹣2
,﹣2![]() +2).
+2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
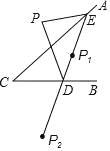
【题目】如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数1个1,2个![]() ,3个
,3个![]() ,…,n个
,…,n个![]() (n为正整数)顺次排成一列:1,
(n为正整数)顺次排成一列:1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,记a1=1,a2=
,…,记a1=1,a2=![]() ,a3=
,a3=![]() ,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知蜗牛从![]() 点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“-”,从开始到结束爬行的各段路程(单位:
点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“-”,从开始到结束爬行的各段路程(单位:![]() )依次为:+7,-5,-10,-8,+9,-6,+12,+4.
)依次为:+7,-5,-10,-8,+9,-6,+12,+4.
(1)若![]() 点在数轴上表示的数为-3,则蜗牛停在数轴上何处,请通过计算加以说明;
点在数轴上表示的数为-3,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)蜗牛在(1)题在数轴上停的位置作以下运动:第1次向左移动1个单位长度至![]() 点,第2次从
点,第2次从![]() 点向右移动2个单位长度至
点向右移动2个单位长度至![]() 点,第3次从
点,第3次从![]() 点向左移动3个单位长度至
点向左移动3个单位长度至![]() 点,第4次从
点,第4次从![]() 点向右移动4个单位长度至
点向右移动4个单位长度至![]() 点,…,依此类推.这样第2019次移动到的点在数轴上表示的数为(请直接写出答案).
点,…,依此类推.这样第2019次移动到的点在数轴上表示的数为(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一,所谓“作差法”:就是通过作差、变形,并利用差的符号来确定它们的大小,要比较代数式![]() 、
、![]() 的大小,只要作出它们的差
的大小,只要作出它们的差![]() ,若
,若![]() ,则
,则![]() .若
.若![]() ,则
,则![]() .若
.若![]() ,则
,则![]() .
.
问题解决:
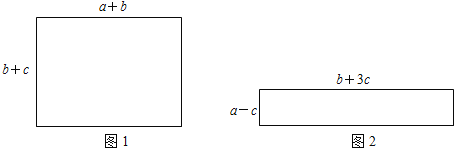
如图,试比较图①、图②两个矩形的周长![]() 、
、![]() 的大小
的大小![]() ;
;
主图形得:![]() ;
;![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,则
,则![]() ;
;
类比应用:
(1)用材料介绍的“作差法”比较![]() 与
与![]() 的大小;
的大小;
联系拓展:
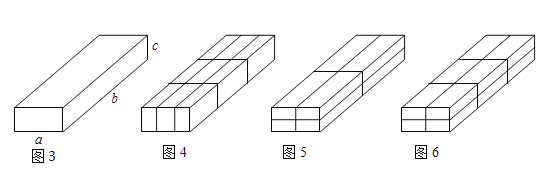
(2)小刚在超市里买了一些物品,用一个长方体的箱子“打包”,这个箱子的尺寸如图3所示(其中![]() ),售货员分别可按图4、图5、图6三种方法进行捆绑,问哪种方法用绳最短?哪种方法用绳最长?请说明理由.
),售货员分别可按图4、图5、图6三种方法进行捆绑,问哪种方法用绳最短?哪种方法用绳最长?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费=自来水销售费用+污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
17吨及以下 | a | 0.80 |
超过17吨不超过30吨的部分 | b | 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a,b的值.
(2)小王家6月份交水费184元,则小王家6月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
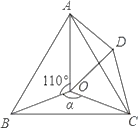
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com