练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

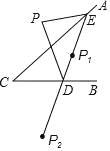
    【题目】如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为_____.

    【答案】4.5

    【解析】

    利用轴对称图形的性质得出PE=EP1，PD=DP2，进而利用DE=4cm，得出P1D的长，即可得出P1P2的长．

    ∵点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上，

    ∴PE=EP1,PD=DP2，

    ∵PE=2.5cm，PD=3cm，DE=4cm，

    ∴P2D=3cm,EP1=2.5cm，

    即DP1=DEEP1=42.5=1.5(cm)，

    则线段P1P2的长为：P1D+DP2=1.5+3=4.5(cm).

    故答案为4.5.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，中，，，的角平分线交于于点，点为上一点，且，，交于点.

    （1）求的度数；

    （2）若，求的长度

    （3）若于点，证明：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂生产的件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人，甲加工新产品的数量要比乙多.

    (1)求甲、乙两人各需加工多少件新产品；

    (2)已知乙比甲平均每天少加工件新产品，用时比甲多用天时间.求甲平均每天加工多少件新产品.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）已知： ，求的值为_____；

    （2）当式子有最大值时，最大值是 ．

    （3）材料：在学习绝对值时，我们知道了绝对值的几何含义，如|5-3|表示5、3在数轴上对应的两点之间的距离：|5+3|=|5-(-3)|，所以|5+3|表示5、-3在数轴上对应的两点之间的距离：那么的最小值是

    （4）求的最小值以及取最小值时的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的一元二次方程.

    （1）试证明：无论取何值此方程总有两个实数根；

    （2）若原方程的两根，满足，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇，如表是近两周的销售情况：（进价、售价均保持不变，利润=销售收入﹣进货成本）

    销售时段

    销售数量

    销售收入

    A种型号

    种型号

    第一周

    3台

    4台

    1200元

    第二周

    5台

    6台

    1900元

    （1）求A、B两种型号的电风扇的销售单价；

    （2）若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？

    （3）在（2）的条件下，超市销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

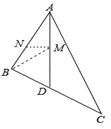
    【题目】如图，在△ABC中，AD平分∠BAC交BC于点D，点M，N分别是AD和AB上的动点，当S△ABC＝12，AC＝8时，BM+MN的最小值等于_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

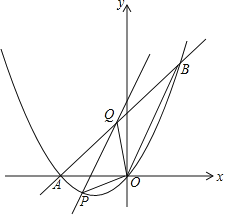
    【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴交于原点及点A，且经过点B（4，8），对称轴为直线x=﹣2．

    （1）求抛物线的解析式；

    （2）设直线y=kx+4与抛物线两交点的横坐标分别为x1，x2（x1＜x2），当时，求k的值；

    （3）连接OB，点P为x轴下方抛物线上一动点，过点P作OB的平行线交直线AB于点Q，当S△POQ：S△BOQ=1：2时，求出点P的坐标．

    （坐标平面内两点M（x1，y1），N（x2，y2）之间的距离MN=）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】瑞士的一位中学教师巴尔末从光谱数据，，，…中，成功地发现了其规律，从而得到了巴尔末公式，继而打开了光谱奥妙的大门．请你根据这个规律写出第6个数为____．

    查看答案和解析>>

    同步练习册答案