
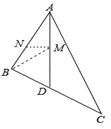
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,点M,N分别是AD和AB上的动点,当S△ABC=12,AC=8时,BM+MN的最小值等于_____.
【答案】3
【解析】
作点B关于AD的对称点B′,过点B′作B′N⊥AB于N交AD于M,由轴对称确定最短路线问题,点M即为使BM+MN最小的点,算出B′N即可
解:如图,作点B关于AD的对称点B′
∵AD是∠BAC的平分线,
∴点B关于AD的对称点B′在AC上,
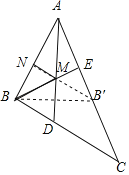
过点B′作B′N⊥AB于N交AD于M,
由轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,
过点B作BE⊥AC于E,
∵AC=8,S△ABC=20,
∴![]() ×8BE=12,
×8BE=12,
解得BE=3,
∵AD是∠BAC的平分线,B′与B关于AD对称,
∴AB=AB′,
∴△ABB′是等腰三角形,
∴B′N=BE=3,
即BM+MN的最小值是3.
故答案为:3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
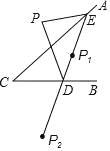
【题目】如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B在坐标轴上,其中A(0,![]() )、B(
)、B(![]() ,0)满足:
,0)满足:![]()
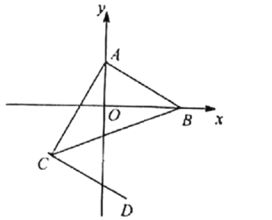
(1)求A、B两点的坐标;
(2)将线段AB平移到CD,点A的对应点为C(-2,t),如图(1)所示.若三角形ABC的面积为9,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数1个1,2个![]() ,3个
,3个![]() ,…,n个
,…,n个![]() (n为正整数)顺次排成一列:1,
(n为正整数)顺次排成一列:1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,记a1=1,a2=
,…,记a1=1,a2=![]() ,a3=
,a3=![]() ,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一,所谓“作差法”:就是通过作差、变形,并利用差的符号来确定它们的大小,要比较代数式![]() 、
、![]() 的大小,只要作出它们的差
的大小,只要作出它们的差![]() ,若
,若![]() ,则
,则![]() .若
.若![]() ,则
,则![]() .若
.若![]() ,则
,则![]() .
.
问题解决:
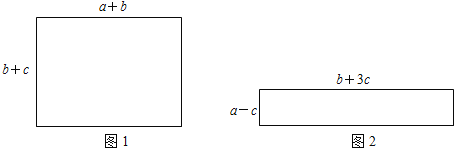
如图,试比较图①、图②两个矩形的周长![]() 、
、![]() 的大小
的大小![]() ;
;
主图形得:![]() ;
;![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,则
,则![]() ;
;
类比应用:
(1)用材料介绍的“作差法”比较![]() 与
与![]() 的大小;
的大小;
联系拓展:
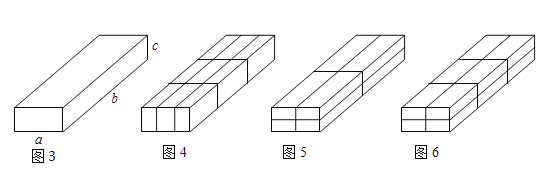
(2)小刚在超市里买了一些物品,用一个长方体的箱子“打包”,这个箱子的尺寸如图3所示(其中![]() ),售货员分别可按图4、图5、图6三种方法进行捆绑,问哪种方法用绳最短?哪种方法用绳最长?请说明理由.
),售货员分别可按图4、图5、图6三种方法进行捆绑,问哪种方法用绳最短?哪种方法用绳最长?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三条公路两两相交,交点分别为A、B、C,现计划修一个油库,要求到三条公路的距离相等,可供选择的地址有( )

A. 一处 B. 二处 C. 三处 D. 四处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com