
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 , x2 , 且x12+x22=10,求实数a的值.
【答案】
(1)解:证明:△=(a+3)2﹣4(a+1)
=a2+6a+9﹣4a﹣4
=a2+2a+5
=(a+1)2+4,
∵(a+1)2≥0,
∴(a+1)2+4>0,即△>0,
∴方程总有两个不相等的实数根;
(2)解:根据题意得x1+x2=﹣(a+3),x1x2=a+1,
∵x12+x22=10,
∴(x1+x2)2﹣2x1x2=10,
∴(a+3)2﹣2(a+1)=10,
整理得a2+4a﹣3=0,解得a1=﹣2+ ![]() ,a2=﹣2﹣
,a2=﹣2﹣ ![]() ,
,
即a的值为﹣2+ ![]() 或﹣2﹣
或﹣2﹣ ![]() .
.
【解析】(1)先求得一元二次方程根的判别式△=a2+2a+5,然后再利用配方法可求得△>0,从而可得到问题的答案;
(2)先依据一元二次方程根与系数的关系得到x1+x2=﹣(a+3),x1x2=a+1,然后依据平方公式可得到(x1+x2)2﹣2x1x2=10,从而可得到关于a的一元二次方程,于是可求得a的值.
【考点精析】掌握求根公式和根与系数的关系是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的个数是( )

①图甲,DE⊥AC,BF⊥AC
②图乙,DE平分∠ADC,BF平分∠ABC
③图丙,E是AB的中点,F是CD的中点
④图丁,E是AB上一点,EF⊥AB.
A. 3个B. 4个C. 1个D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
(1)补全坐标系并指出△ABC和△A'B'C'满足什么几何变换(直接写答案)?
(2)作△A'B'C'关于x轴对称图形△A''B''C'';
(3)△ABC和△A''B''C''满足什么几何变换?求A''、B''、C''三点坐标(直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(x﹣1)2+k分别与x轴、y轴交于A、B、C三点,点A在点B的左侧,直线y=﹣ ![]() x+2经过点B,且与y轴交于点D.
x+2经过点B,且与y轴交于点D.
(1)如图1,求k的值;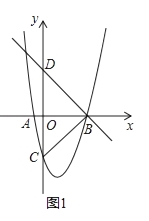
(2)如图2,在第一象限的抛物线上有一动点P,连接AP,过P作PE⊥x轴于点E,过E作EF⊥AP于点F,过点D作平行于x轴的直线分别与直线FE、PE交于点G、H,设点P的横坐标为t,线段GH的长为d,求d与t的函数关系式,并直接写出t的取值范围;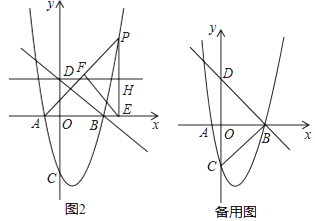
(3)在(2)的条件下,过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N,tan∠MEA= ![]() ,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com