
【题目】二次函数y=(x﹣1)2+k分别与x轴、y轴交于A、B、C三点,点A在点B的左侧,直线y=﹣ ![]() x+2经过点B,且与y轴交于点D.
x+2经过点B,且与y轴交于点D.
(1)如图1,求k的值;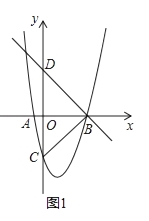
(2)如图2,在第一象限的抛物线上有一动点P,连接AP,过P作PE⊥x轴于点E,过E作EF⊥AP于点F,过点D作平行于x轴的直线分别与直线FE、PE交于点G、H,设点P的横坐标为t,线段GH的长为d,求d与t的函数关系式,并直接写出t的取值范围;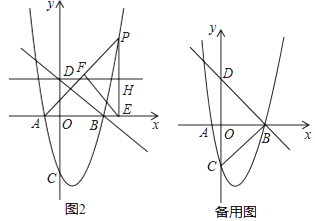
(3)在(2)的条件下,过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N,tan∠MEA= ![]() ,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
【答案】
(1)解:在一次函数y=﹣ ![]() x+2中,令y=0,得:0=﹣
x+2中,令y=0,得:0=﹣ ![]() x+2,
x+2,
解得x=3,
∴B(3,0).
令x=0得y=2,
∴D(0,2).
将B(3,0),代入y=(x﹣1)2+k得:4+k=0,
∴k=﹣4.
(2)解:如答图1所示:
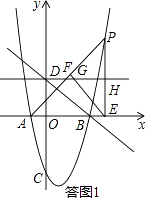
∵PE⊥x轴,EF⊥AP,
∴∠PEA=∠EFA=90°
∵∠PEF+∠FEA=90°,∠PAE+∠FEA=90°
∴∠PEF=∠PAE.
∵DH∥x轴 HE⊥x轴
∴∠HDO=∠DOE=∠PEO=90°
∴四边形DOEH为矩形.
∴HE=2.
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
∴d=2t﹣6.(t>3).
(3)解:∵∠TGH=∠GTE=∠TEH=90°,
∴GHET为矩形.
∴GH=d=ET=2t﹣6.
∵tan∠MEB= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴MT=3t﹣9.
∵ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() ,
,
解得t=4.
∴P(4,5).
∴AT=AE﹣ET=t+1﹣(2t﹣6)=7﹣t=3.
∴M(2,3)
把x=2代入y=x2﹣2x﹣3中,得N(2,﹣3)
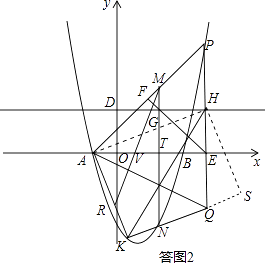
∴MT=TN=AT,∠MAT=90°.
∵∠RAE﹣∠RMA=45°,
∴∠RAE﹣45°=∠RMA,
∴∠RAM=∠RMA,
∵S△AKQ=S△HKQ,作HW⊥KQ.
∴AK∥HW,AK=HW,
∴四边形AKWH是矩形,
∴∠RAH=∠HAK=90°,
∴∠RAM=∠HAN.
∵A(﹣1,0),H(4,2),N(2,﹣3),
∴AH=HN= ![]() ,
,
∴∠HAN=∠HNA=∠RAM=∠RMA.
又∵AM=AN,
∴△RAM≌△HAN,
∴AR=AH.
过R作RL⊥x轴,
∴∠RLA=∠AEH=90°,
∵∠RAL+∠HAE=90,∠HAE+∠AHE=90,
∴∠RAL=∠AHE,
∴△ARL≌△AHE.
∴RL=AE=5,AL=HE=3
∴R(﹣3,5).
由∠RAM﹣∠RMA=45°可知∠RAV=∠RVA,∠RMT=∠HAE,tan∠RMT=tan∠HAE= ![]() ,V(
,V( ![]() ,0),
,0),
直线MR的解析式为y= ![]() x﹣2,直线AK的解析式为y=﹣
x﹣2,直线AK的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
交点R(﹣ ![]() ,
, ![]() ).
).
【解析】(1)先求出一次函数与两坐标轴的交点B、D的坐标,再将点B的坐标代入二次函数解析式即可求得k的值。
(2)根据已知PE⊥x轴,EF⊥AP,得出∠PEA=∠EFA=90°,再根据同角的余角相等,证得∠PEF=∠PAE.根据矩形的性质得出HE=2.然后利用三角形函数的定义得出线段成比例,建立方程,可求出d与t的函数关系式及x的取值范围。
(3)利用(2)中求得的函数关系式,根据矩形的性质及三角函数的定义先求出点P和点M的坐标,由MN平行y轴,因此将x=2代入二次函数解析式,即可求得点N的坐标,即可得出MT=TN=AT,添加辅助线作HS⊥KQ.去证明四边形AKSH是矩形,推出∠RAM=∠HAN,再证明△RAM≌△HAN,得出AR=AH.过R作RL⊥x轴,易正明△ARL≌△AHE.得出RL=AE=5,AL=HE=3,可得到点R的坐标,再求出直线MR的解析式和直线AK的解析式,即可求出两直线的交点R的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 , x2 , 且x12+x22=10,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《重庆市生活垃圾分类管理办法》于2019年开始实施我校为积极响应政府对垃圾分类处理的号召,开展了垃圾分类网上知识竞赛,并从该校七年级随机抽取了部分学生的竞赛成绩进行整理、描述和分析(根据成绩共分![]() 四个等级),其中获得
四个等级),其中获得![]() 等级和
等级和![]() 等级的人数相等.
等级的人数相等.
下面给出了相应的条形统计图和扇形统计图:

根据以上信息,解答下列问题:
(1)共抽取了______名学生;
(2)补全条形统计图,并求出扇形统计图中![]() 等级对应的圆心角的度数;
等级对应的圆心角的度数;
(3)A等级中有![]() 名同学是女生,学校计划从
名同学是女生,学校计划从![]() 等级的学生中抽取
等级的学生中抽取![]() 名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少?
名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AD是BC边上的中线,有以下结论:①AD平分∠BAC;②△ABD的周长-△ACD的周长=AB-AC;③BC=2AD;④△ABD的面积是△ABC面积的一半.其中正确的是( )

A.①②④B.②③④C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,EF∥AB,DE:AE=2:3,△BDC的面积为25,则四边形AEFB的面积为( )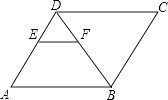
A.25
B.9
C.21
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水
(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?
请用尺规作图,将上述两种情况下的自来水厂厂址分别在图(1)(2)中标出,并保留作图痕迹。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列资料,并解决问题.
地球上的水包括大气水、地表水和地下水三大类,地表水可以分为海洋水和陆地水,陆地水又可分为冰川、河流、湖泊等。地球上的水总体积是14.2亿![]() ,其中,海洋水约占96.53%以上,淡水约占2.53%,而在淡水中,大部分在两极的冰川、冰盖和地下水的形式存在,其中冰川、冰盖占77.2%,地下水占22.4%,而人类可以利用的水还不到1%.
,其中,海洋水约占96.53%以上,淡水约占2.53%,而在淡水中,大部分在两极的冰川、冰盖和地下水的形式存在,其中冰川、冰盖占77.2%,地下水占22.4%,而人类可以利用的水还不到1%.
我国是世界上严重缺水的国家之一,年水资源总量居世界第六位,人均占有水量仅为![]() 左右,只相当于世界人均的
左右,只相当于世界人均的![]() ,居世界第110位,中国已被联合国列为13个贫水国之一.
,居世界第110位,中国已被联合国列为13个贫水国之一.
图1是我国2006年至2015年水资源总量变动趋势图,全国用水量由农业用水、工业用水、生活用水和生态补水四部分组成,表1是2015年我国四类用水量统计表.

表1 2015年四类用水统计表
用水类别 | 用水量(亿立方米) | 所占百分比 |
农业用水 | 3903.9 | 63.17% |
工业用水 | 1380.6 | 22.34% |
生活用水 | 790.5 | 12.79% |
生态补水 | 105.0 | 1.70% |
解决问题:
(1)根据国外的经验,一个国家的用水量超过其水资源总量20%,就有可能发生“水危机”.依据这个标准,请你计算2015年我国是否属于可能发生“水危机”行列?
(2)第四十七届联合国大会作出决议,确定每年3月22日为“世界水日”.我国水利部确定每年的3月22日至28日是“中国水周”.我国纪念“世界水日”和“中国水周”宣传活动的主题是“实施国家节水行动,建设节水型社会”.小亮作为学校的节水行动宣传志愿者,对他所在学校部分学生进行了“节水在行动”的随机调查,表2是问卷调查表,并将调查结果绘制成图2和图3所示的统计图(均不完整),请根据统计图提供的信息,解答下列问题:
①参与本次调查的学生人数有________人(直接写出答案);
②补全条形统计图;在扇形统计图中,观点![]() 的百分比是_______(直接写出答案);
的百分比是_______(直接写出答案);
表2:节水问卷调查表 | ||
你好,请在表格中选择一项你对节水的认识,在其后面打“√”,非常感谢你的合作. | ||
代码 | 观点 | |
A | 水费低,不需要节水 | |
B | 节水意识薄弱,认为水资源充足 | |
C | 缺乏社会责任意识,节水与我无关 | |
D | 知道节水的重要性,并有节水的好习惯 | |
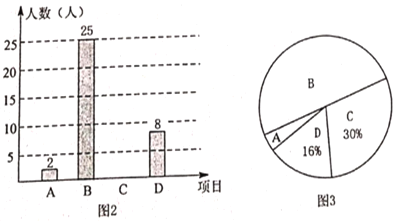
③若该学校共有800名学生,请估计其中“知道节水的重要性,并有节水的好习惯”的有多少人?
④谈一谈你对节约用水的看法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com