
����Ŀ���Ķ��������ϣ����������.
�����ϵ�ˮ��������ˮ���ر�ˮ�͵���ˮ�����࣬�ر�ˮ���Է�Ϊ����ˮ��½��ˮ��½��ˮ�ֿɷ�Ϊ�����������������ȡ������ϵ�ˮ�������14.2��![]() �����У�����ˮԼռ96.53%���ϣ���ˮԼռ2.53%�����ڵ�ˮ�У����������ı��������Ǻ͵���ˮ����ʽ���ڣ����б���������ռ77.2%������ˮռ22.4%��������������õ�ˮ������1%.
�����У�����ˮԼռ96.53%���ϣ���ˮԼռ2.53%�����ڵ�ˮ�У����������ı��������Ǻ͵���ˮ����ʽ���ڣ����б���������ռ77.2%������ˮռ22.4%��������������õ�ˮ������1%.
�ҹ�������������ȱˮ�Ĺ���֮һ����ˮ��Դ�������������λ���˾�ռ��ˮ����Ϊ![]() ���ң�ֻ�൱�������˾���
���ң�ֻ�൱�������˾���![]() ���������110λ���й��ѱ����Ϲ���Ϊ13��ƶˮ��֮һ.
���������110λ���й��ѱ����Ϲ���Ϊ13��ƶˮ��֮һ.
ͼ1���ҹ�2006����2015��ˮ��Դ�����䶯����ͼ��ȫ����ˮ����ũҵ��ˮ����ҵ��ˮ��������ˮ����̬��ˮ�IJ�����ɣ���1��2015���ҹ�������ˮ��ͳ�Ʊ�.

��1 2015��������ˮͳ�Ʊ�
��ˮ��� | ��ˮ��(��������) | ��ռ�ٷֱ� |
ũҵ��ˮ | 3903.9 | 63.17% |
��ҵ��ˮ | 1380.6 | 22.34% |
������ˮ | 790.5 | 12.79% |
��̬��ˮ | 105.0 | 1.70% |
������⣺
(1)���ݹ���ľ��飬һ�����ҵ���ˮ��������ˮ��Դ����20%�����п��ܷ�����ˮΣ����.������������������2015���ҹ��Ƿ����ڿ��ܷ�����ˮΣ�������У�
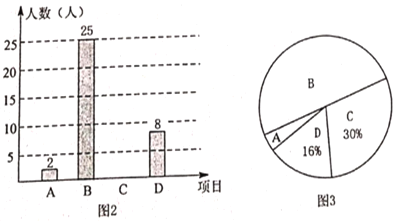
(2)����ʮ�߽����Ϲ�����������飬ȷ��ÿ��3��22��Ϊ������ˮ����.�ҹ�ˮ����ȷ��ÿ���3��22����28�������й�ˮ����.�ҹ�����������ˮ���������й�ˮ�������������������ʵʩ���ҽ�ˮ�ж��������ˮ�������.С����ΪѧУ�Ľ�ˮ�ж�����־Ը�ߣ���������ѧУ����ѧ������������ˮ���ж�����������飬��2���ʾ���������������������Ƴ�ͼ2��ͼ3��ʾ��ͳ��ͼ(��������)�������ͳ��ͼ�ṩ����Ϣ������������⣺
�ٲ��뱾�ε����ѧ��������________��(ֱ��д����)��
�ڲ�ȫ����ͳ��ͼ��������ͳ��ͼ�У��۵�![]() �İٷֱ���_______(ֱ��д����)��
�İٷֱ���_______(ֱ��д����)��
��2����ˮ�ʾ������ | ||
��ã����ڱ�����ѡ��һ����Խ�ˮ����ʶ�������������̡����dz���л��ĺ���. | ||
���� | �۵� | |
A | ˮ�ѵͣ�����Ҫ��ˮ | |
B | ��ˮ��ʶ��������Ϊˮ��Դ���� | |
C | ȱ�����������ʶ����ˮ������ | |
D | ֪����ˮ����Ҫ�ԣ����н�ˮ�ĺ�ϰ�� | |
������ѧУ����800��ѧ���������������֪����ˮ����Ҫ�ԣ����н�ˮ�ĺ�ϰ�������ж����ˣ�
��̸һ̸��Խ�Լ��ˮ�Ŀ���.
���𰸡�(1)2015���ҹ����ڿ��ܷ�����ˮΣ�������У�(2)��50���ڲ�ͼ��������4%����128�ˣ��ܼ�����.
��������
��1����2015�����ˮ������2015���ˮ��Դ������20���Ƚϼ��������жϣ�
��2������D���ֵ���������D���ֵİٷֱȼ��ɣ�����50��ȥA��B��D�����������C����������A����������50��������۵�![]() �İٷֱȣ�����800����D�İٷֱȼ��ɣ������ˮ��ʶ�йؼ��ɣ��𰸲�Ψһ.
�İٷֱȣ�����800����D�İٷֱȼ��ɣ������ˮ��ʶ�йؼ��ɣ��𰸲�Ψһ.
�⣺(1)2015�����ˮ��Ϊ��3903.9+1380.6+790.5+105.0=6180(��������)
��ˮ��Դ�����䶯����ͼ�ɵ�2015���ˮ��Դ����Ϊ28306(��������)��
![]() ��
��
![]() ��
��
��2015���ҹ����ڿ��ܷ�����ˮΣ��������.
(2)��8��16��=50�ˣ�
��50-2-25-8=5�ˣ�2��50=4%��
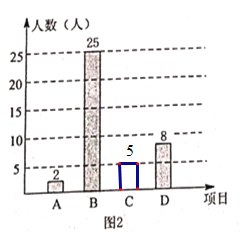
�۽⣺![]() (��)
(��)
�𣺹���������128��֪����ˮ����Ҫ�Բ��н�ˮ�ĺ�ϰ�ߣ�
�ܴ�ͨ��������Կ�������ˮ��ʶ��������Ϊˮ��Դ����������ȱ�����������ʶ��ˮ��������ռ����������16%��ͬѧ�н�ˮ�ĺ�ϰ�ߡ���ȫ��ˮ��Դ��ȱ�������ҹ�ˮ��ԴΣ���������ص�����£���Լ��ˮӦ��������ÿλ��������������Σ�ͬʱ����Ҫ���ý�ˮ������������ֻ������13���������������������𣬰ѽ�ˮ�䵽ʵ�������ܱ�������̺����������ü�.(�𰸲�Ψһ�����ո���)


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=��x��1��2+k�ֱ���x�ᡢy�ύ��A��B��C���㣬��A�ڵ�B����ֱ࣬��y=�� ![]() x+2������B������y�ύ�ڵ�D��
x+2������B������y�ύ�ڵ�D��
��1����ͼ1����k��ֵ��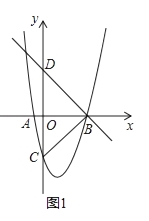
��2����ͼ2���ڵ�һ��������������һ����P������AP����P��PE��x���ڵ�E����E��EF��AP�ڵ�F������D��ƽ����x���ֱ�߷ֱ���ֱ��FE��PE���ڵ�G��H�����P�ĺ�����Ϊt���߶�GH�ij�Ϊd����d��t�ĺ�����ϵʽ����ֱ��д��t��ȡֵ��Χ��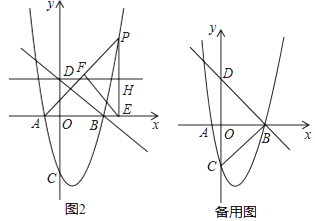
��3���ڣ�2���������£�����G��ƽ����y���ֱ�߷ֱ�AP��x����������ڵ�M��T��N��tan��MEA= ![]() ����KΪ����������������һ�㣬���ڶԳ�����࣬����KA��������KA��ȡһ��R������RM������K��KQ��AK��PE���ӳ�����Q������AQ��HK������RAE����RMA=45�㣬��AKQ���HKQ�������ȣ����R�����꣮
����KΪ����������������һ�㣬���ڶԳ�����࣬����KA��������KA��ȡһ��R������RM������K��KQ��AK��PE���ӳ�����Q������AQ��HK������RAE����RMA=45�㣬��AKQ���HKQ�������ȣ����R�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�˲���ij�����ĸ߶ȣ�С���ó�Ϊ2m��������������ߣ��ƶ���ͣ�ʹ��Ͷ��˵�Ӱ�������Ķ��˵�Ӱ��ǡ�����ڵ����ͬһ�㣮��ʱ�������һ�����5m���������10m�������ĸ߶�Ϊ�� ��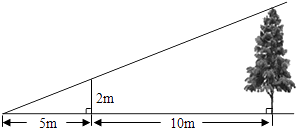
A.5m
B.6m
C.7m
D.8m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������ABCD�����Ϊ12,��ABC�ǵȱ�������,��E��������ABCD��,�Խ���AC����һ��PʹPE+PD�ĺ���С,�����СֵΪ( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
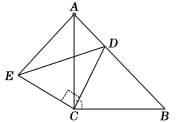
����Ŀ����ͼ����ACB����ECD���ǵ���ֱ�������Σ���ACB=��ECD=90����DΪAB����һ�㣮
��֤����1����ACE�ա�BCD����2��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
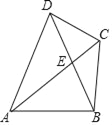
����Ŀ����ͼ�����ı���ABCD�У�AB��BC���Խ���AC��BD�ཻ�ڵ�E��EΪBD�е㣬��AD��BD��AB��2����BAC��30�㣬��DC��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʽ�ֽ⣺
��1�����㣺
��![]() ����(��2x��y)(y��2x)��(2x+y)2��
����(��2x��y)(y��2x)��(2x+y)2��
��2����ʽ�ֽ⣺
��2x2��4x+2����a2(x��y)+9b2(y��x)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������г���λ�����С��������ʱ���Խ��Ƶؿ�������洹ֱ��չ��С���������ᱣ��ˮƽ������ͼ1��ͼ2�ֱ���С��������ʱ��չ��ʱ��ʵ�ͼ3�е�ʵ����С����չ�����ʾ��ͼ������OB��ʾС��������Ŀ��ȣ�BC��ʾС�����֧�ܣ�����OA����ʱOA=75���ף���AOB=��ACB=37�㣬��֧�ܳ�BC�������OB�ij���֮�͵���OA�ij��ȣ����B��AC�ľ��룮���ο�����sin37���0.6��cos37���0.8��tan37���0.75��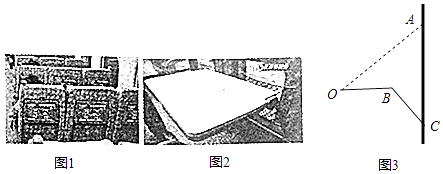
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ȤС�������һ����¥AB�ĸ߶ȣ���ͼ����¥ǰ��һ��б��BC����֪BC�ij�Ϊ12�ף������¶�i=1�� ![]() ������C��40��D�����ò���Dz�ô�¥����A������Ϊ37�㣬�����DE�ĸ�Ϊ1.5�ף����¥AB�ĸ߶�ԼΪ�����ף��������ȷ��0.1�ף�
������C��40��D�����ò���Dz�ô�¥����A������Ϊ37�㣬�����DE�ĸ�Ϊ1.5�ף����¥AB�ĸ߶�ԼΪ�����ף��������ȷ��0.1�ף�
���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75�� ![]() ��1.73����
��1.73����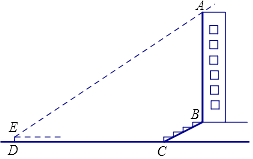
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com