
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动. 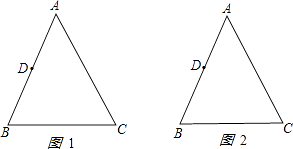
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
【答案】
(1)解:经过1秒后,PB=3cm,PC=5cm,CQ=3cm, 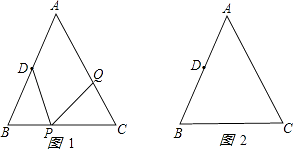
∵△ABC中,AB=AC,
∴在△BPD和△CQP中,
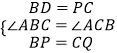 ,
,
∴△BPD≌△CQP(SAS)
(2)解:设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等;则可知PB=3tcm,PC=8﹣3tcm,CQ=xtcm,
∵AB=AC,
∴∠B=∠C,
根据全等三角形的判定定理SAS可知,有两种情况:①当BD=PC,BP=CQ时,②当BD=CQ,BP=PC时,两三角形全等;
①当BD=PC且BP=CQ时,8﹣3t=5且3t=xt,解得x=3,∵x≠3,∴舍去此情况;
②BD=CQ,BP=PC时,5=xt且3t=8﹣3t,解得:x= ![]() ;
;
故若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为 ![]() cm/s时,能够使△BPD与△CQP全等
cm/s时,能够使△BPD与△CQP全等
【解析】(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,由已知可得BD=PC,BP=CQ,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP.(2)可设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等,则可知PB=3tcm,PC=8﹣3tcm,CQ=xtcm,据(1)同理可得当BD=PC,BP=CQ或BD=CQ,BP=PC时两三角形全等,求x的解即可.


科目:初中数学 来源: 题型:
【题目】若a=﹣2×32 , b=(﹣2×3)2 , c=﹣(2×3)2 , 则下列大小关系中正确的是( )
A.a>b>c
B.b>c>a
C.b>a>c
D.c>a>b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 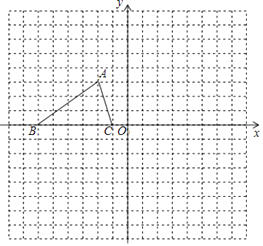
(1)将△ABC沿y轴翻折,则翻折后点A的对应点的坐标是 .
(2)作出△ABC关于y轴对称的图形△A1B1C1 , 画△A1B1C1 , 并直接写出点A1的坐标.
(3)将△ABC向下平移平移6个单位,向右平移7个单位得到△A2B2C2 , 画出平移后的图形.
(4)若以D,B,C为顶点的三角形与△ABC全等,请画出所有符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
一列火车要以每秒20米的速度通过第一、第二两座铁桥(火车的长度忽略不计)过第二座铁桥比过第一座铁桥多50秒,已知铁桥的长度比第一座铁桥的长度的两倍短500米,求两座铁桥各自的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com