
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )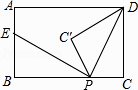
A.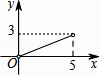
B.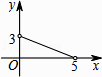
C.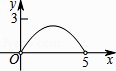
D.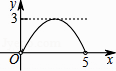
【答案】C
【解析】解:由翻折的性质得,∠CPD=∠C′PD,
∵PE平分∠BPC1 ,
∴∠BPE=∠C′PE,
∴∠BPE+∠CPD=90°,
∵∠C=90°,
∴∠CPD+∠PDC=90°,
∴∠BPE=∠PDC,
又∵∠B=∠C=90°,
∴△PCD∽△EBP,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴y= ![]() x(5﹣x)=﹣
x(5﹣x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴函数图象为C选项图象.
故选:C.
根据翻折变换的性质可得∠CPD=∠C′PD,根据角平分线的定义可得∠BPE=∠C′PE,然后求出∠BPE+∠CPD=90°,再根据直角三角形两锐角互余求出∠CPD+∠PDC=90°,从而得到∠BPE=∠PDC,根据两组角对应相等的三角形相似求出△PCD和△EBP相似,根据相似三角形对应边成比例列式求出y与x的关系式,再根据二次函数的图象解答即可.


科目:初中数学 来源: 题型:
【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解题过程并回答问题.
解方程:![]() .
.
解:①当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() .经检验,符合题意;
.经检验,符合题意;
②当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() .经检验,x的值不合题意,舍去;
.经检验,x的值不合题意,舍去;
③当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() 音.经检验,符合题意.
音.经检验,符合题意.
所以原方程的解是![]() 或
或![]() .
.
(1)根据上面的解题过程,求方程![]() 的解;
的解;
(2)根据上面的解题过程,求方程![]() 的解;
的解;
(3)方程![]() 解.(填“有”或“无”)
解.(填“有”或“无”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70.
⑴请写出AB的中点M对应的数
![]()
⑵现在有一只电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2个单位/秒的速度向左运动,设两只电子蚂蚁在数轴上的C点相遇,请你求出C点对应的数 .
⑶若当电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2单位/秒的速度向左运动,经过多长时间两只电子蚂蚁在数轴上相距35个单位长度,并写出此时P点对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地上网有两种收费方式,用户可以任选其一:
(A)记时制:2.8元/小时,
(B)包月制:16元/月.此外,每一种上网方式都加收通讯费1.2元/小时.
(1)某用户上网20小时,选用哪种上网方式比较合算?
(2)当上网时间在什么小时时,两种上网费用一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD//OB,则图中休闲区(阴影部分)的面积是( ) 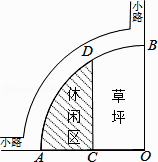
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

查看答案和解析>>
科目:初中数学 来源: 题型:
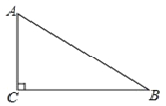
【题目】如图,在 ABC ,C 90,AC<BC,D 为 BC 上一点,且到 A、B 两点的距离相等.
(1)用直尺和圆规,作出点 D 的位置(不写作法,保留作图痕迹);
(2)连结 AD,若 B 36 ,求∠CAD 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com