
【题目】某地上网有两种收费方式,用户可以任选其一:
(A)记时制:2.8元/小时,
(B)包月制:16元/月.此外,每一种上网方式都加收通讯费1.2元/小时.
(1)某用户上网20小时,选用哪种上网方式比较合算?
(2)当上网时间在什么小时时,两种上网费用一样多?
【答案】(1)上网时间20小时时,选择包月制比较合算;(2)![]() 小时时,两种费用一样多.
小时时,两种费用一样多.
【解析】
记时制的费用为: (2.8+通讯费) ![]() 上网时间;包月制的费用为:16+通讯费
上网时间;包月制的费用为:16+通讯费![]() 上网时间;
上网时间;
(1) 把上网时间20小时代入两种费用求值, 比较即可;
(2) 让两种费用相等列式求值可得上网时间在什么小时时, 两种上网费用一样多.
解:(1)当上网时间为20时,记时制的费用为:(2.8+1.2)×20=80元,
包月制的费用为:16+1.2×20=40元,
∴上网时间20小时时,选择包月制比较合算;
(2)解:x小时时,两种上网费用一样多,
(2.8+1.2)x=16+1.2x,
解得x=![]() .
.
答:![]() 小时时,两种费用一样多.
小时时,两种费用一样多.


科目:初中数学 来源: 题型:
【题目】冰封超市购进一批运动服,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每套运动服的售价为140元.
(1)求每套运动服的进价?
(2)超市卖出一半后,正好赶上双十一促销,商店决定将剩下的运动服每3套400元的价格出售,很快销售一空,这批运动服超市共获利14000元,求该超市共购进多少套运动服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,![]() ,
,![]() ,动点
,动点![]() 在
在![]() 轴的上方,且满足
轴的上方,且满足![]() .
.
(1)若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )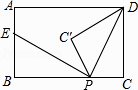
A.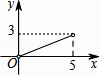
B.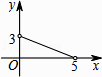
C.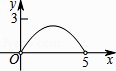
D.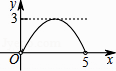
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的变形规律:
![]() ;
;![]() ;
;![]() ;….
;….
解答下面的问题:
(1)仿照上面的格式请写出![]() = ;
= ;
(2)若n为正整数,请你猜想![]() = ;
= ;
(3)基础应用:计算:![]() .
.
(4)拓展应用1:解方程:![]() =2016
=2016
(5)拓展应用2:计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
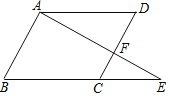
【题目】如图,若∠DAE=∠E,∠B=∠D,那么AB∥DC吗?请在下面的解答过程中填空或在括号内填写理由.
解:理由如下:
∵∠DAE=∠E,________
∴______∥BE,________
∴∠D=∠DCE.________
又∵∠B=∠D,________
∴∠B=______.(等量代换)
∴______∥______,(同位角相等,两直线平行)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com