
【题目】小明同学骑自行车去郊外春游,如图为表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象. 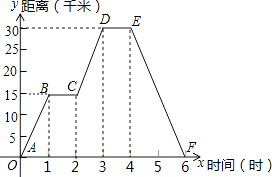
(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?
(2)求小明出发2.5小时离家多远?
(3)求小明出发多长时间距家10千米.
【答案】
(1)解:由图象可知小明到达离家最远的地方需3小时;
此时他离家30千米
(2)解:设直线CD的解析式为y=k1x+b1,由C(2,15)、D(3,30),
代入得: ![]() ,
,
解得: ![]() ,
,
故直线CD的解析式为:y=15x﹣15,(2≤x≤3)
当x=2.5时,y=22.5.
答:出发两个半小时,小明离家22.5千米
(3)解:设过E、F两点的直线解析式为y=k2x+b2,
由E(4,30)、F(6,0),代入得
![]() ,
,
解得: ![]() ,
,
故直线EF的解析式为:y=﹣15x+90,(4≤x≤6)
过A、B两点的直线解析式为y=k3x,
∵B(1,15),
∴y=15x(0≤x≤1)
分别令y=10,则10=﹣15x+90,10=15x,
解得:x= ![]() ,x=
,x= ![]() ,
,
答:小明出发 ![]() 小时或
小时或 ![]() 小时距家10千米
小时距家10千米
【解析】(1)根据分段函数的图象上点的坐标的意义可知:小明到达离家最远的地方需3小时;此时,他离家30千米;(2)因为C(2,15)、D(3,30)在直线上,运用待定系数法求出解析式后,把x=2.5代入解析式即可;(3)分别利用待定系数法求得过E、F两点的直线解析式,以及A、B两点的直线解析式.分别令y=10,求解x.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
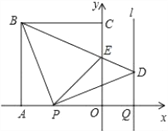
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
(1)∠PBD的度数为 ,点D的坐标为 (用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)6.25×(﹣3.4)+6.25×4.4
(3)![]()
(4)![]()
(5)(﹣1)2015﹣(1﹣0.5)2×|2﹣22|
(6)﹣1+2﹣3+4﹣…﹣2015+2016.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列几种运动属于平移的是( )
①水平运输带上的砖的运动;②啤酒生产线上的啤酒通过压盖机前后的运动;③升降机上下做机械运动;④足球场上足球的运动
A. 一种 B. 两种 C. 三种 D. 四种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级上学期期中考试后从全年级400名学生中抽取了60名学生的考试成绩作为一个样本,用来分析全年级的考试成绩情况,这个问题的样本容量是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC. 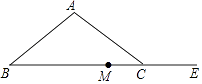
(1)尺规作图:作∠ABC的平分线,交AC于点D(保留作图痕迹,不写作法);
(2)E是底边BC的延长线上一点,M是BE的中点,连接DE、DM.若CE=CD,求证:DM⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b是实数,x=a2+b2+24,y=2(3a+4b),则x,y的大小关系是( )
A. x≤y B. x≥y C. x<y D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com