
【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= ______ °时,四边形BECD是矩形.

【答案】(1)证明见解析;(2)100
【解析】(1)证明:∵四边形ABCD为平行四边形,∴AB∥DC,AB=CD,∴∠OEB=∠ODC,又∵O为BC的中点,∴BO=CO,在△BOE和△COD中,∵∠OEB=∠ODC,∠BOE=∠COD,BO=CO,∴△BOE≌△COD(AAS);
∴OE=OD,∴四边形BECD是平行四边形;
(2)解:若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.理由如下:
∵四边形ABCD是平行四边形,∴∠BCD=∠A=50°,∵∠BOD=∠BCD+∠ODC,∴∠ODC=100°﹣50°=50°=∠BCD,∴OC=OD,∵BO=CO,OD=OE,∴DE=BC,∵四边形BECD是平行四边形,∴四边形BECD是矩形;
故答案为:100.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
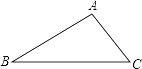
【题目】已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2![]() ,
,
求:(1)AB的长为________;
(2)S△ABC=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校开展了以“梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品.现将从中挑选的50件参赛作品的成绩(单位:分)统计如下:
等级 | 成绩(用m表示) | 频数 | 频率 |
A | 90≤m≤100 | x | 0.08 |
B | 80≤m<90 | 34 | y |
C | m<80 | 12 | 0.24 |
合计 | 50 | 1 |
请根据上表提供的信息,解答下列问题:
(1)表中x的值为 , y的值为;(直接填写结果)
(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3…表示.现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,则恰好抽到学生A1和A2的概率为 . (直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
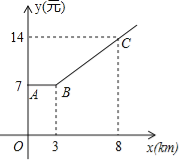
(1)根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(2)某人乘坐13km,应付多少钱?
(3)若某人付车费42元,出租车行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下列证明过程补充完整:
已知:如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2
求证:∠E=∠F

证明:∵∠BAP+∠APD=180°(已知)
∴ ∥ ( )
∴∠BAP= ( )
又∵∠1=∠2(已知)
∴∠BAP﹣ = ﹣∠2
即∠3= (等式的性质)
∴AE∥PF( )
∴∠E=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com